Level 3
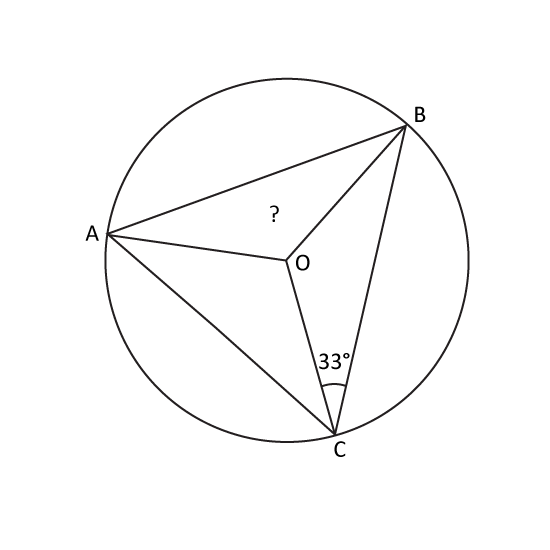
In the figure, not drawn to scale, O is the centre of the circle. Given that the ratio of ∠OBC : ∠AOC is 3 : 11. Find ∠AOB.
Level 3
In the figure, not drawn to scale, O is the centre of the circle. Given that the ratio of ∠OBC : ∠AOC is 3 : 11. Find ∠AOB.
Image in this question is not available.
Level 3
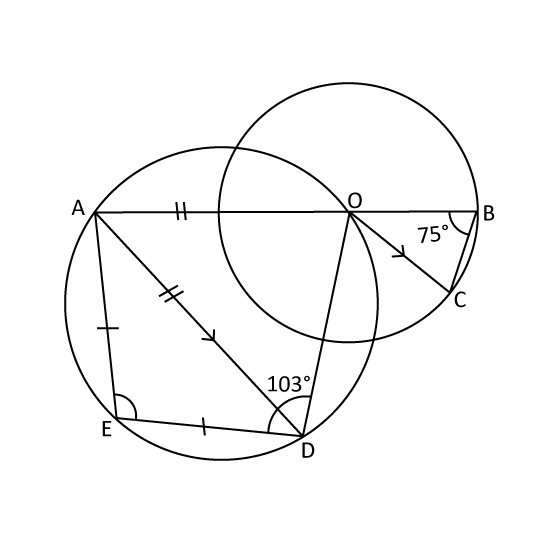
In the figure, not drawn to scale, O is the centre of the smaller circle. AB is a straight line. Find ∠AED.
Level 3
In the figure, not drawn to scale, O is the centre of the smaller circle. AB is a straight line. Find ∠AED.
Image in this question is not available.
Level 3 PSLE
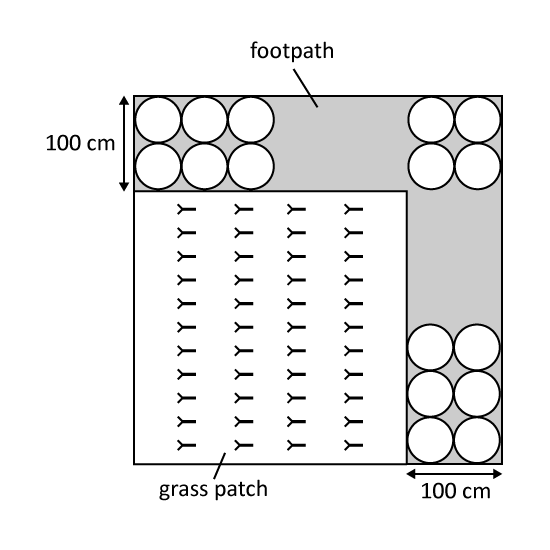
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Level 3 PSLE
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Image in this question is not available.
Level 3
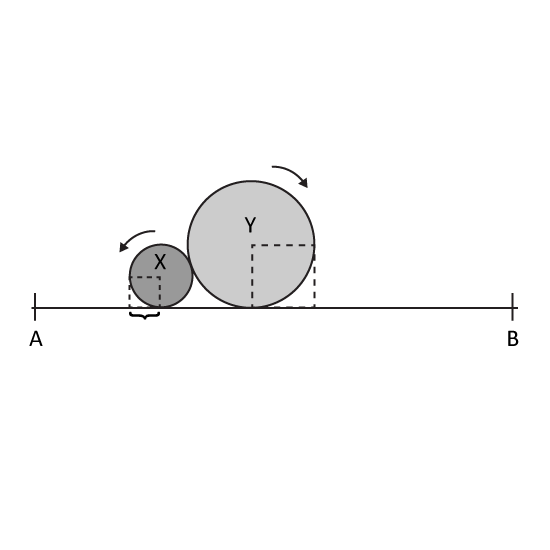
The figure is not drawn to scale. Two balls, X and Y, turn and move along the line AB in opposite directions. The radius of X is 10 cm. The ratio of the diameter of Ball X to that of Ball Y is 5 : 2. If Ball X turns 10 rounds and Ball Y turns 2 rounds, how far apart are the centres of the balls?
(Take π = 3.14)
Level 3
The figure is not drawn to scale. Two balls, X and Y, turn and move along the line AB in opposite directions. The radius of X is 10 cm. The ratio of the diameter of Ball X to that of Ball Y is 5 : 2. If Ball X turns 10 rounds and Ball Y turns 2 rounds, how far apart are the centres of the balls?
(Take π = 3.14)
Image in this question is not available.
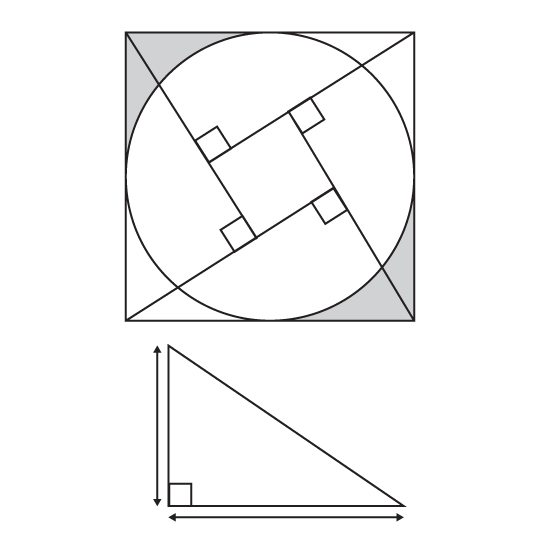
Level 3
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Level 3
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Image in this question is not available.
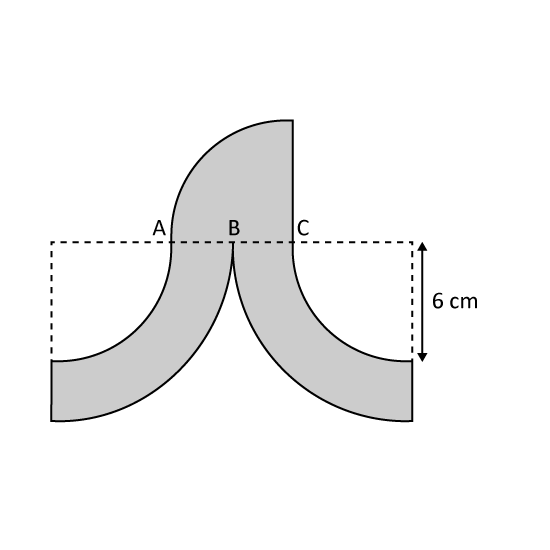
Level 2 PSLE The outline of the shaded figure is formed by 3 identical small quarter circles, 2 identical large quarter circles and 3 straight lines. Take π = 3.14
- What is the radius of the large quarter circle?
- Find the perimeter of the shaded figure.
Level 2 PSLE The outline of the shaded figure is formed by 3 identical small quarter circles, 2 identical large quarter circles and 3 straight lines. Take π = 3.14
- What is the radius of the large quarter circle?
- Find the perimeter of the shaded figure.
Image in this question is not available.
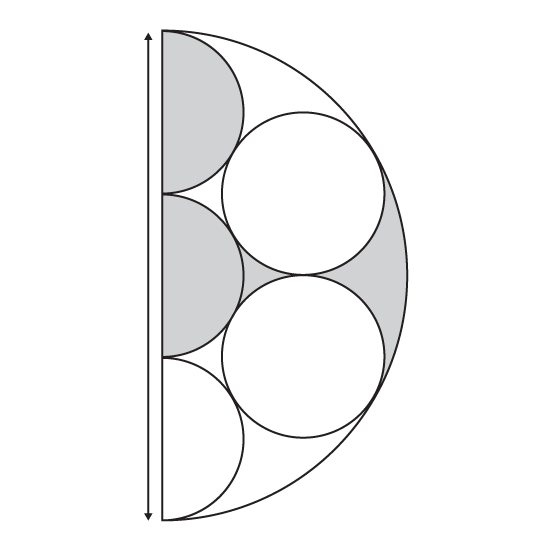
Level 3
A piece of rope is used to make the figure shown. Inside the big semicircle are 2 small circles and 3 small semi-circles, all of which have the same radius. The diameter of the big semicircle is 30 cm. Find the area of the shaded region. (Leave the answer in terms of π)
Level 3
A piece of rope is used to make the figure shown. Inside the big semicircle are 2 small circles and 3 small semi-circles, all of which have the same radius. The diameter of the big semicircle is 30 cm. Find the area of the shaded region. (Leave the answer in terms of π)
Image in this question is not available.
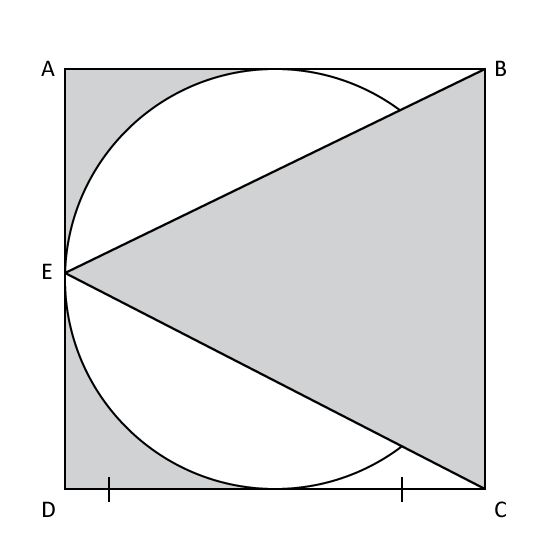
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Image in this question is not available.
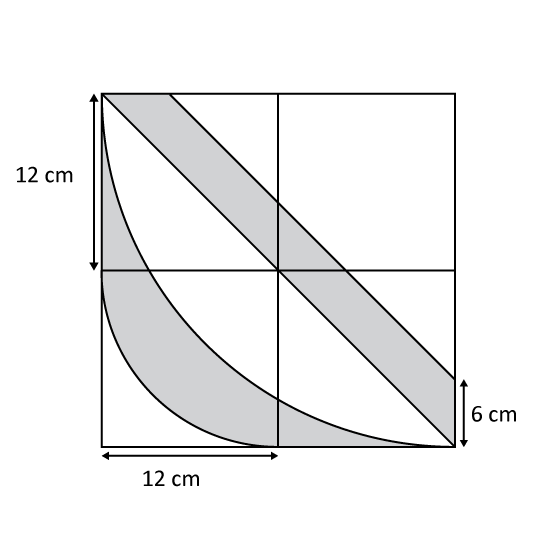
Level 3
Willi noticed the patterns on the square tiles and tried to calculate the area of the shaded part. Leave the answer in 2 decimal places.
(Take π = 3.14)
Level 3
Willi noticed the patterns on the square tiles and tried to calculate the area of the shaded part. Leave the answer in 2 decimal places.
(Take π = 3.14)
Image in this question is not available.
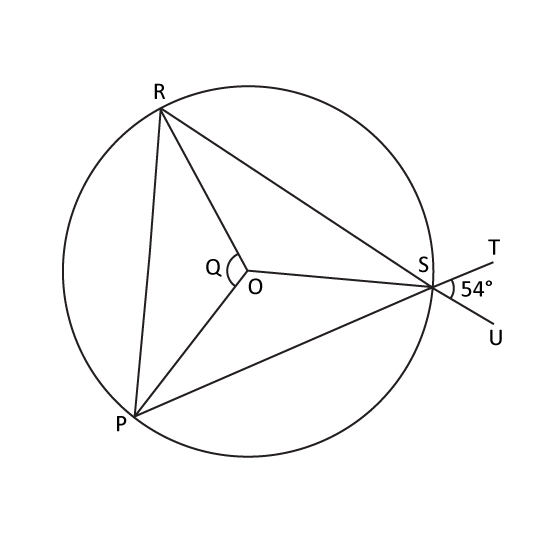
Level 3
In the figure not drawn to scale, O is the centre of the circle and RSU and PST are straight lines. If ∠TSU = 54° and ∠RSO is twice of ∠OSP, find ∠Q.
Level 3
In the figure not drawn to scale, O is the centre of the circle and RSU and PST are straight lines. If ∠TSU = 54° and ∠RSO is twice of ∠OSP, find ∠Q.
Image in this question is not available.