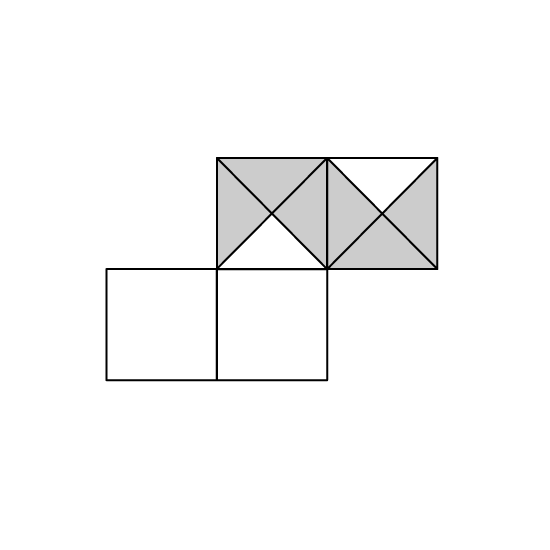
Level 1 PSLE
The figure is made up of 4 squares. Two of the squares are divided equally into 4 triangles each. What fraction of the figure is shaded?
Level 1 PSLE
The figure is made up of 4 squares. Two of the squares are divided equally into 4 triangles each. What fraction of the figure is shaded?
Image in this question is not available.
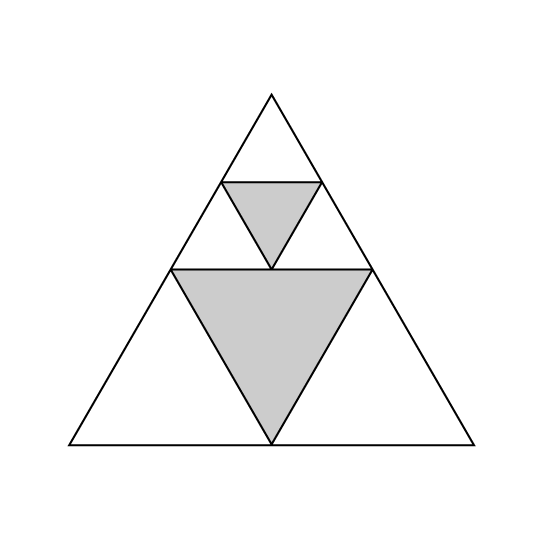
Level 1 PSLE
The figure is made up of equilateral triangles. What fraction of the figure is shaded?
Level 1 PSLE
The figure is made up of equilateral triangles. What fraction of the figure is shaded?
Image in this question is not available.
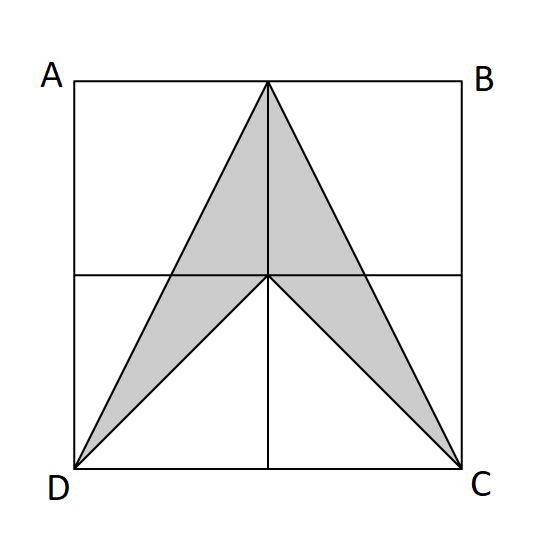
Level 2 PSLE
The square ABCD is made up of 4 smaller squares.
- What is the ratio of the area of the shaded part to the area of the unshaded part?
- If the length of the square ABCD is 4 cm, what is the area of the shaded part?
Level 2 PSLE
The square ABCD is made up of 4 smaller squares.
- What is the ratio of the area of the shaded part to the area of the unshaded part?
- If the length of the square ABCD is 4 cm, what is the area of the shaded part?
Image in this question is not available.
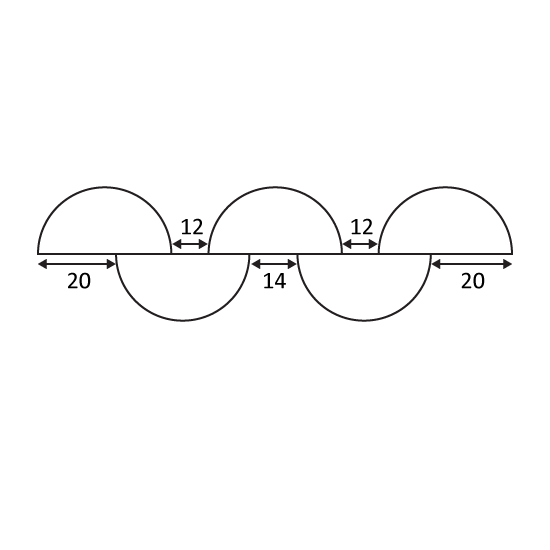
Level 2 PSLE
Five identical semi-circles are arranged as shown. Find the diameter of one circle.
Level 2 PSLE
Five identical semi-circles are arranged as shown. Find the diameter of one circle.
Image in this question is not available.
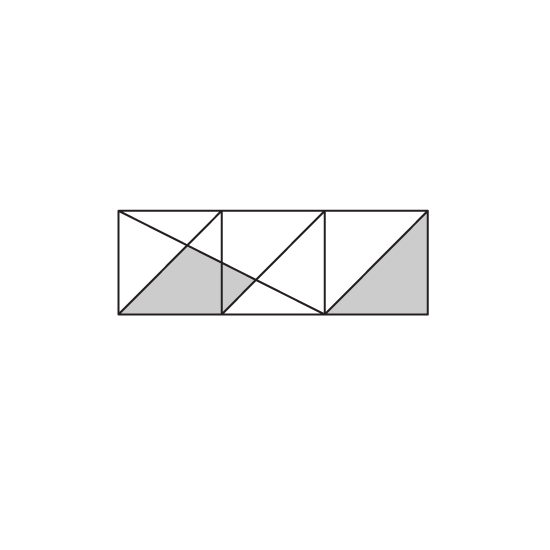
Level 1
What fraction of the figure is shaded?
Level 1
What fraction of the figure is shaded?
Image in this question is not available.
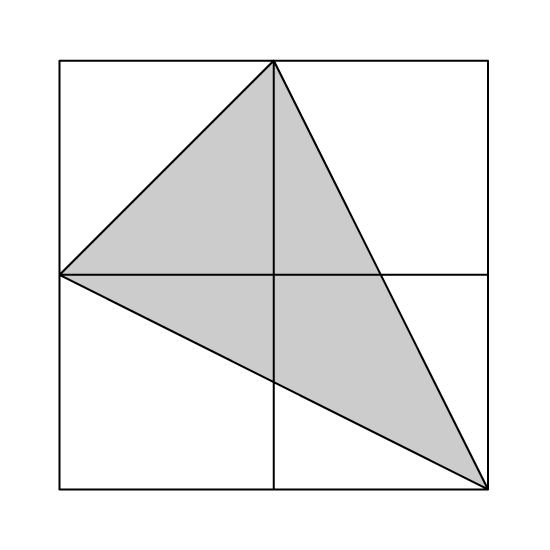
Level 1 PSLE
The figure is made up of three squares ABGH, BCFG, CDEF. What fraction of the figure ADEH is shaded?
Level 1 PSLE
The figure is made up of three squares ABGH, BCFG, CDEF. What fraction of the figure ADEH is shaded?
Image in this question is not available.
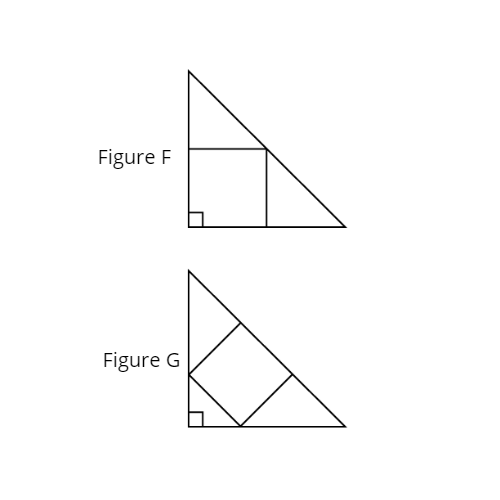
Level 2
The figures F and G, are two identical isosceles triangles. Both figures contain a square of a different size. Given that the area of the square in Figure F is 252 cm2, find the area of the square in Figure G.
Level 2
The figures F and G, are two identical isosceles triangles. Both figures contain a square of a different size. Given that the area of the square in Figure F is 252 cm2, find the area of the square in Figure G.
Image in this question is not available.
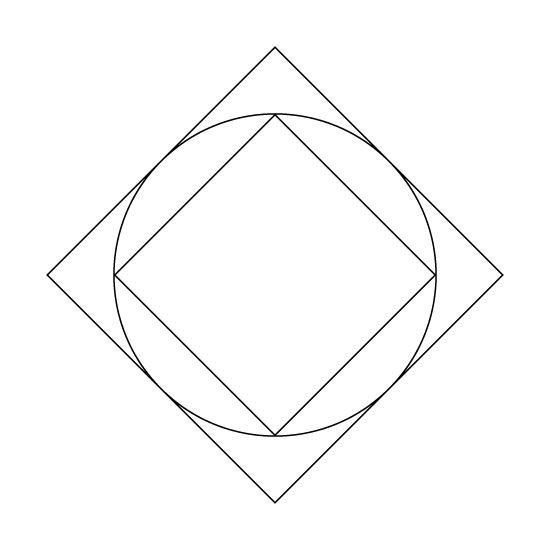
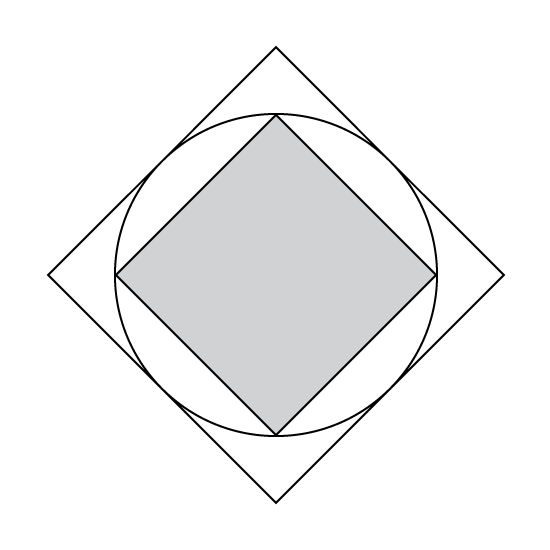
Level 2
In the figure, the circle is touching each of the two squares at exactly four points, if the area of the bigger square is 100 cm2, find the area of the smaller square.
Level 2
In the figure, the circle is touching each of the two squares at exactly four points, if the area of the bigger square is 100 cm2, find the area of the smaller square.
Image in this question is not available.
Level 2
The figure consists of 2 squares and a circle. If the length of the bigger square is 10 cm, what is the area of the shaded part?
Level 2
The figure consists of 2 squares and a circle. If the length of the bigger square is 10 cm, what is the area of the shaded part?
Image in this question is not available.
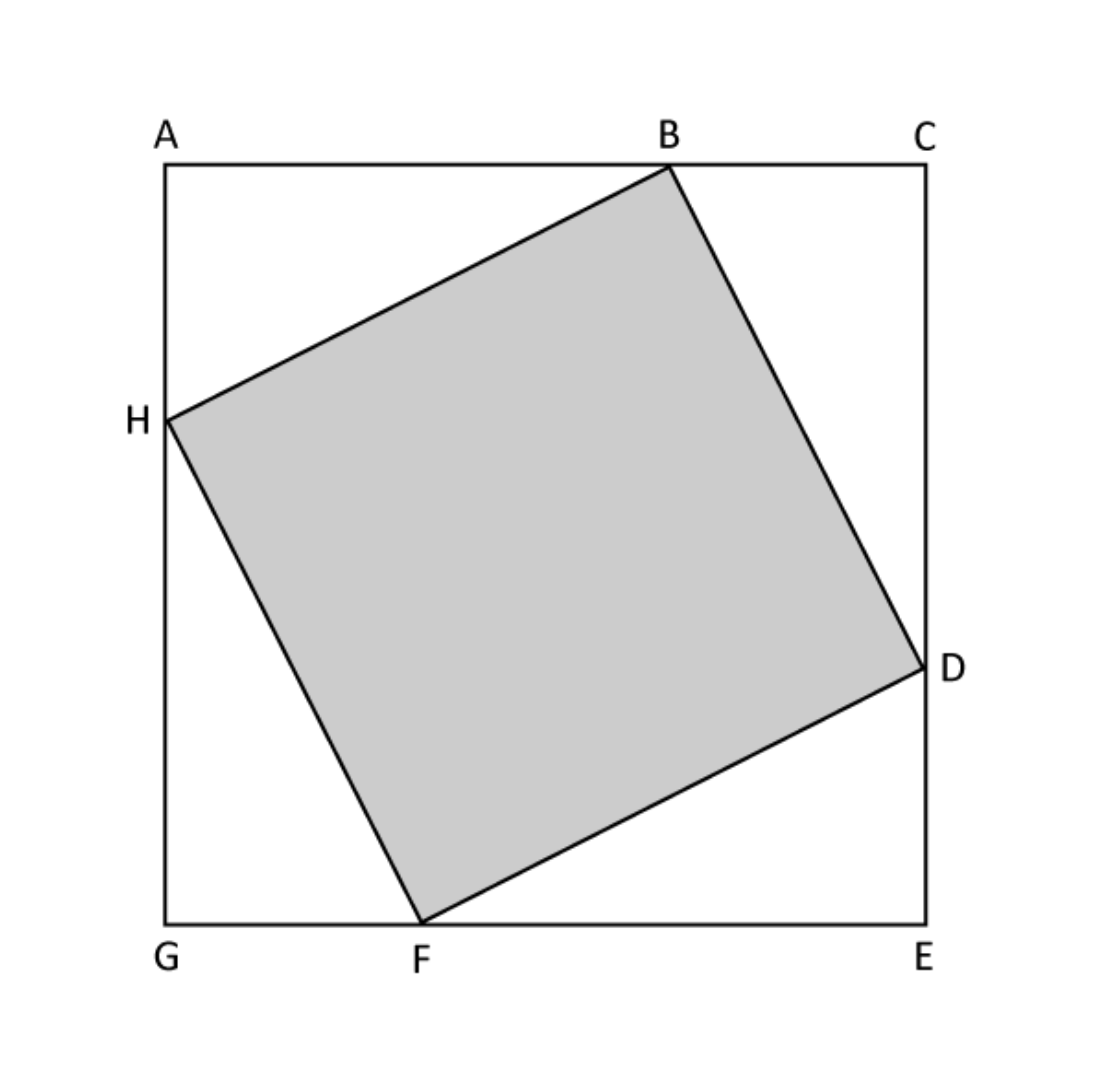
Level 3 PSLE
In the figure not drawn to scale, ACEG and BDFH are squares. AB, CD, EF and GH are of the same length. The ratio of AB : BC is 3 : 1.
- What fraction of square ACEG is shaded?
- If the length of the square is 96 cm, find the unshaded area in cm2.
Level 3 PSLE
In the figure not drawn to scale, ACEG and BDFH are squares. AB, CD, EF and GH are of the same length. The ratio of AB : BC is 3 : 1.
- What fraction of square ACEG is shaded?
- If the length of the square is 96 cm, find the unshaded area in cm2.
Image in this question is not available.