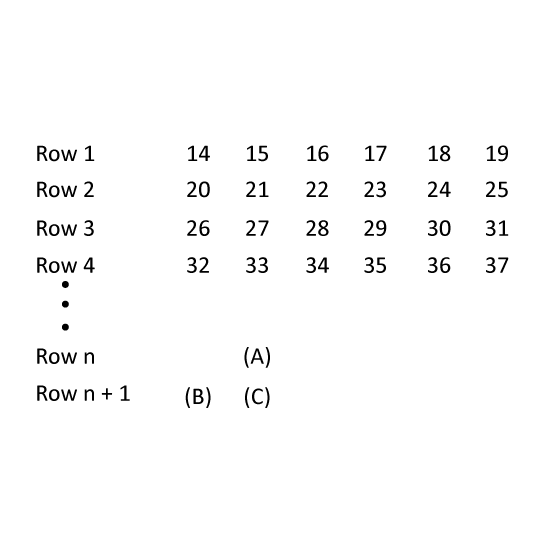
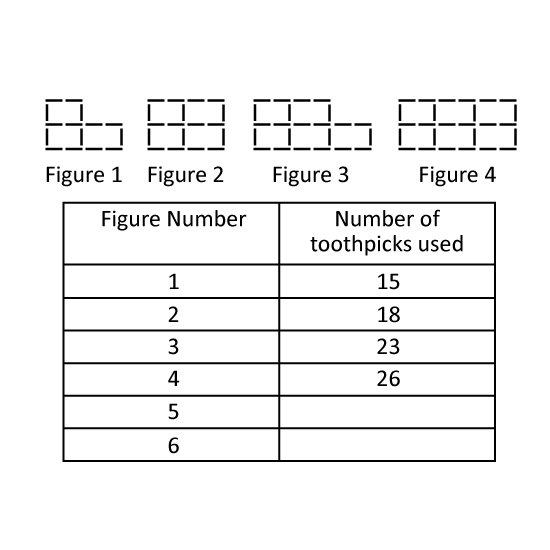
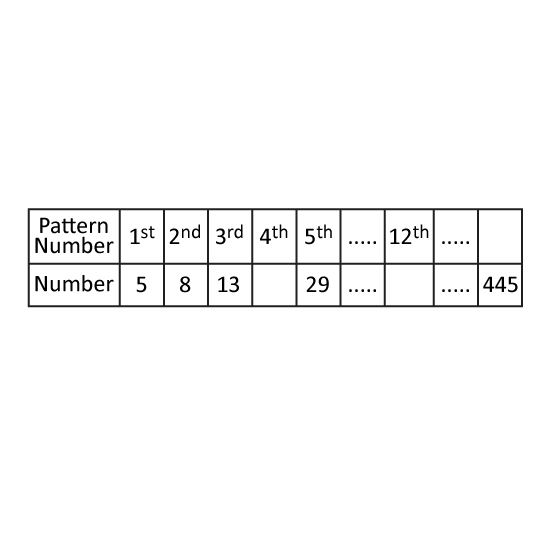
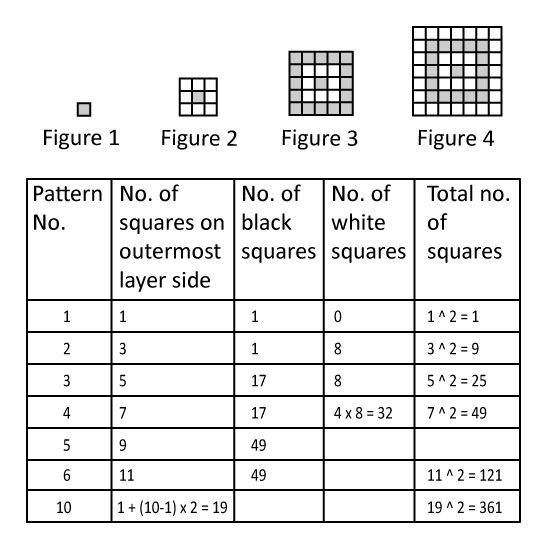
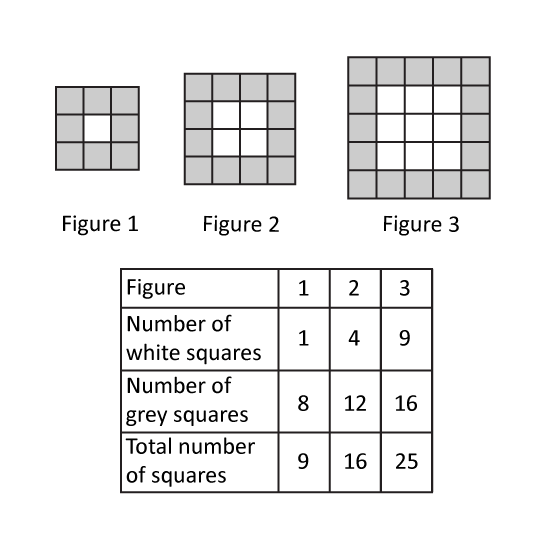
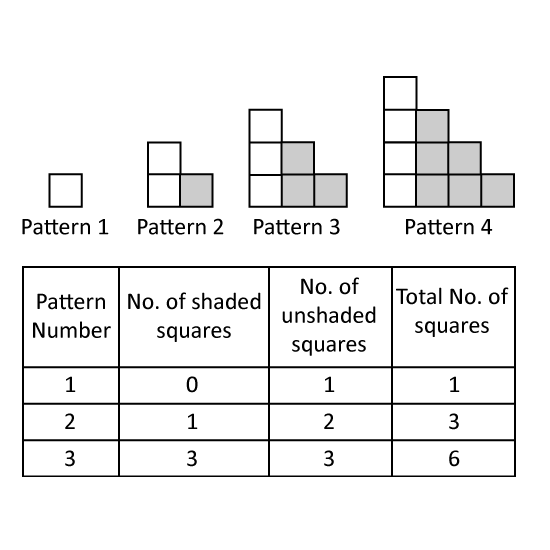
Level 3
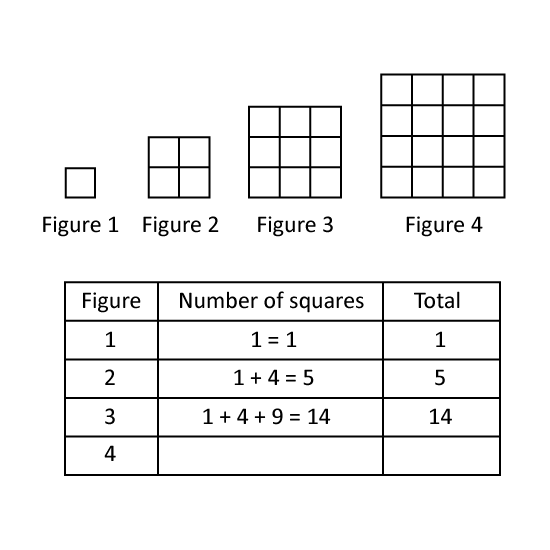
The diagram shows the first four of a sequence of figures.
Figure 1 is made up of just 1 square.
Figure 2 is made up of one 2 x 2 and four 1 x 1 squares, so it has a total of 1 + 4 = 5 squares.
Figure 3 contains one 3 x 3 and some 2 x 2 squares and nine 1 x 1 squares.
The sequence continues as shown in Figure 4 and so on.
- How many squares are there in Figure 7?
- How many total number of squares will be there in sequence 7?
Level 3
The diagram shows the first four of a sequence of figures.
Figure 1 is made up of just 1 square.
Figure 2 is made up of one 2 x 2 and four 1 x 1 squares, so it has a total of 1 + 4 = 5 squares.
Figure 3 contains one 3 x 3 and some 2 x 2 squares and nine 1 x 1 squares.
The sequence continues as shown in Figure 4 and so on.
- How many squares are there in Figure 7?
- How many total number of squares will be there in sequence 7?