Level 3
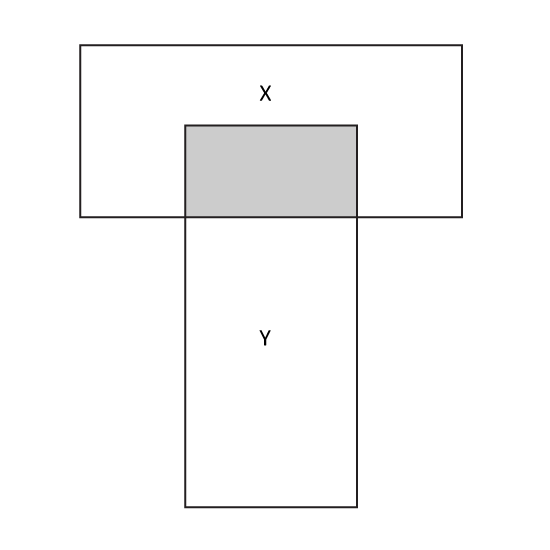
The figure, not drawn to scale, on the right shows 2 rectangles overlapping each other. The ratio of the shaded area to the area of Rectangle X is 4 : 9. The ratio of the shaded area to the area of Rectangle Y is 3 : 6. Find the ratio of the unshaded area to the total area of the figure.
Level 3
The figure, not drawn to scale, on the right shows 2 rectangles overlapping each other. The ratio of the shaded area to the area of Rectangle X is 4 : 9. The ratio of the shaded area to the area of Rectangle Y is 3 : 6. Find the ratio of the unshaded area to the total area of the figure.
Image in this question is not available.
Level 2
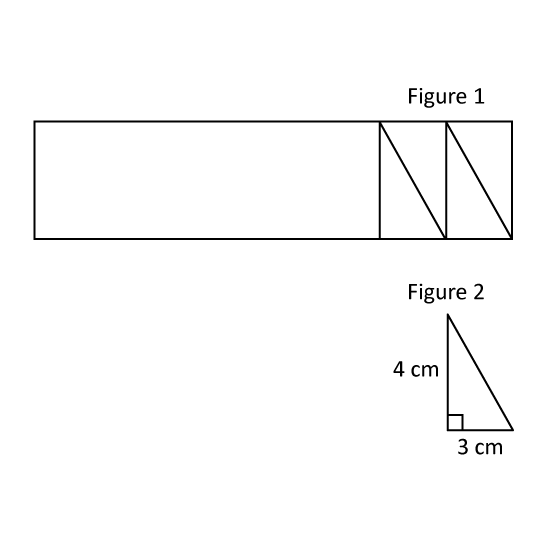
Figure A shows a rectangular sheet of paper. Nellie cut it into 22 identical triangles one of which is shown in
Figure B. There was no paper left over. What was The area of the rectangular sheet of paper before it was cut?
Level 2
Figure A shows a rectangular sheet of paper. Nellie cut it into 22 identical triangles one of which is shown in
Figure B. There was no paper left over. What was The area of the rectangular sheet of paper before it was cut?
Image in this question is not available.
Level 2
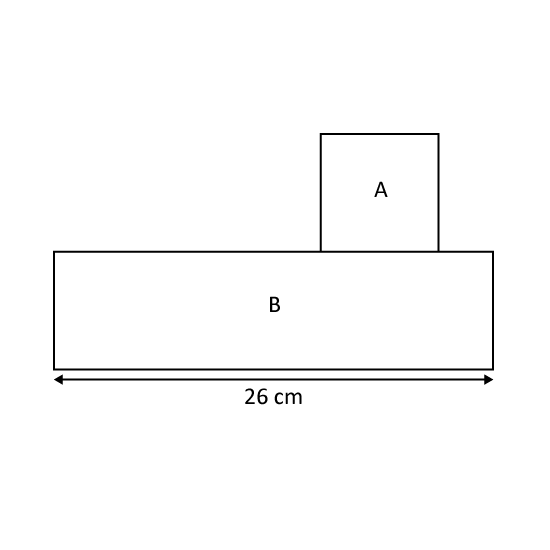
The figure, not drawn to scale, is made up of Square A and Rectangle B. The area of Square A is 49 cm2. The length of Square A is the same as the breadth of Rectangle B. If the length of the Rectangle B is 26 cm, what is the total area of Figure A and B?
Level 2
The figure, not drawn to scale, is made up of Square A and Rectangle B. The area of Square A is 49 cm2. The length of Square A is the same as the breadth of Rectangle B. If the length of the Rectangle B is 26 cm, what is the total area of Figure A and B?
Image in this question is not available.
Level 2
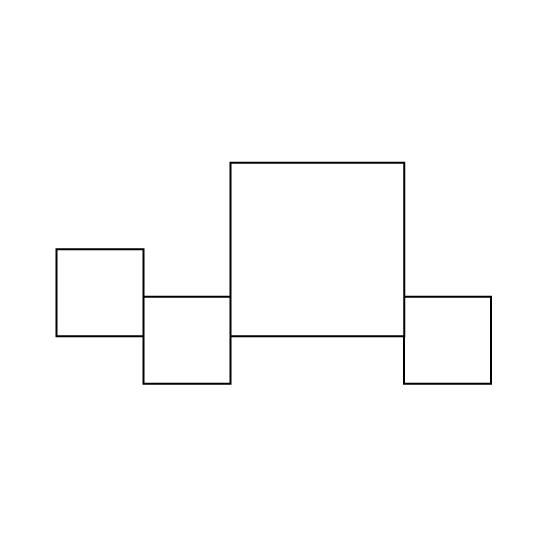
The figure, not drawn to scale, consists of a large square and 3 identical small squares. The side of the large square is twice the side of the small square. If The area of the small square is 4 cm2. Find the area of the figure.
Level 2
The figure, not drawn to scale, consists of a large square and 3 identical small squares. The side of the large square is twice the side of the small square. If The area of the small square is 4 cm2. Find the area of the figure.
Image in this question is not available.
Level 2
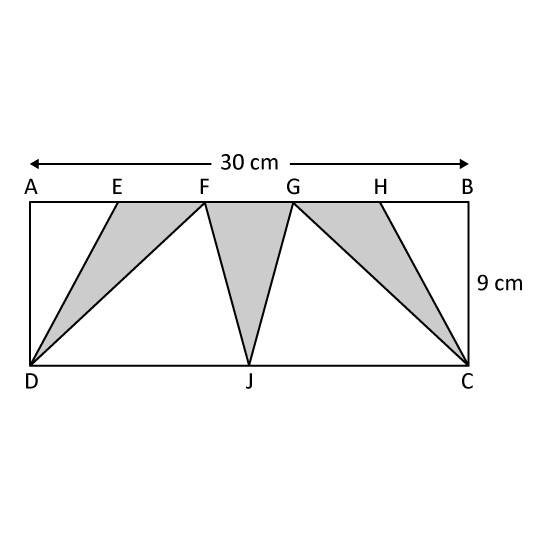
In the figure, ABCD is a rectangle. AE = EF = FG = GH = HB. What is the area of the shaded part?
Level 2
In the figure, ABCD is a rectangle. AE = EF = FG = GH = HB. What is the area of the shaded part?
Image in this question is not available.
Level 1
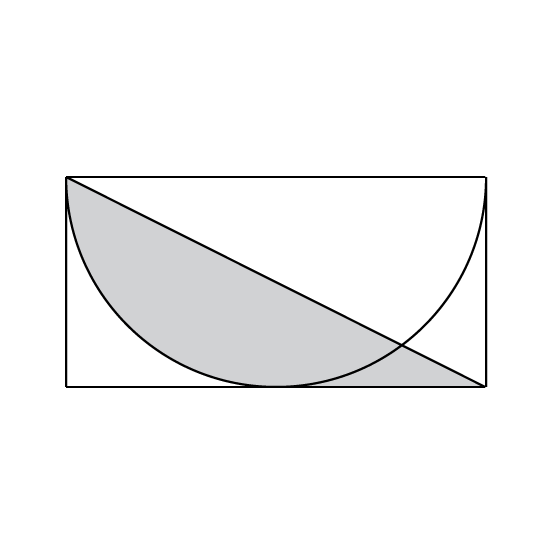
The figure is made up of a rectangle and a semi-circle. The diameter of the circle is 80 cm. Find the area of the shaded part. (Take π = 3.14)
Level 1
The figure is made up of a rectangle and a semi-circle. The diameter of the circle is 80 cm. Find the area of the shaded part. (Take π = 3.14)
Image in this question is not available.
Level 2
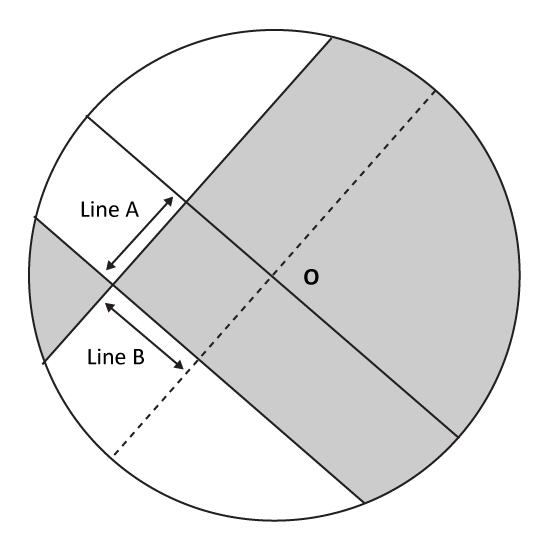
The figure shows a circle with parts of its region shaded. O is the centre of the circle. Line A is 14.3 cm and Line B is 15.8 cm. Find the difference between the shaded and unshaded areas.
Level 2
The figure shows a circle with parts of its region shaded. O is the centre of the circle. Line A is 14.3 cm and Line B is 15.8 cm. Find the difference between the shaded and unshaded areas.
Image in this question is not available.
Level 2
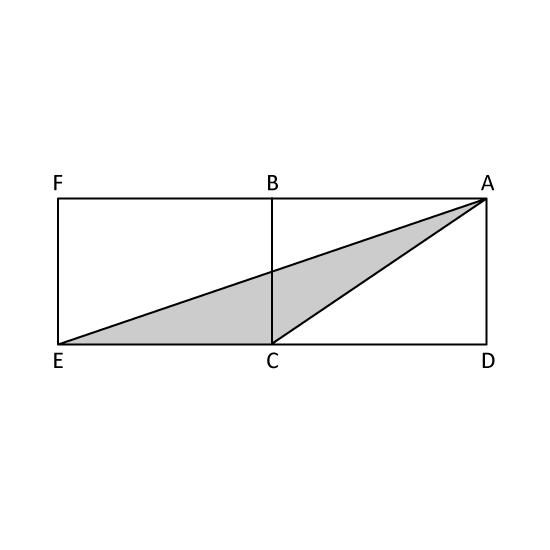
The figure is made up of two identical rectangles ABCD and BCEF. The area of Triangle ACE is 12 the area of Rectangle ______.
Level 2
The figure is made up of two identical rectangles ABCD and BCEF. The area of Triangle ACE is 12 the area of Rectangle ______.
Image in this question is not available.
Level 2
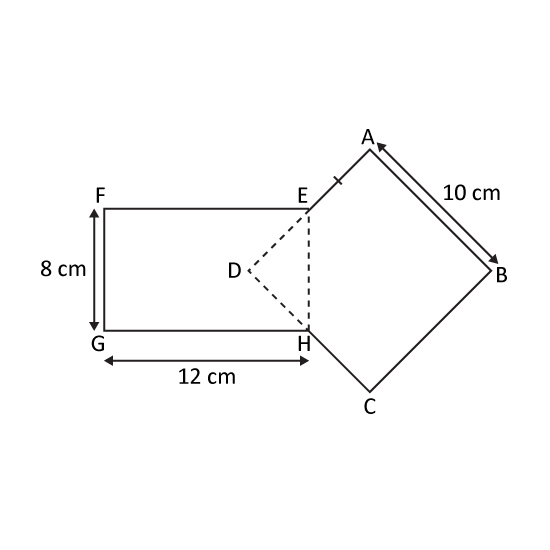
The figure shown is cut from a piece of paper. ABCD is a square and EFGH is a rectangle. Find the area of the figure.
Level 2
The figure shown is cut from a piece of paper. ABCD is a square and EFGH is a rectangle. Find the area of the figure.
Image in this question is not available.
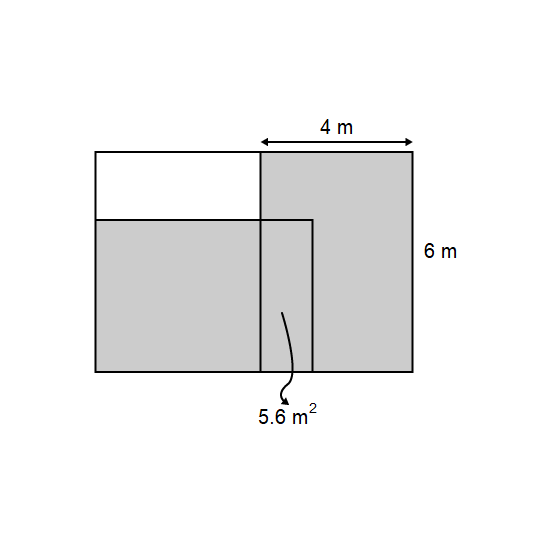
Level 3 PSLE
Two rectangular mats, each 6 m by 4 m, are place on the floor of a rectangular room as shown. The mats overlap. The area of the floor covered by the overlap is 5.6 cm2. Find the area of the floor not covered by the mats.
Level 3 PSLE
Two rectangular mats, each 6 m by 4 m, are place on the floor of a rectangular room as shown. The mats overlap. The area of the floor covered by the overlap is 5.6 cm2. Find the area of the floor not covered by the mats.
Image in this question is not available.
Level 2 PSLEJasmine had a piece of ribbon 17p cm long. She formed a triangle, with sides measuring p cm, 5p cm and 30 cm, with part of the wire.
- Express the length of the remaining ribbon in terms of p in the simplest form.
- Jasmine used the remaining ribbon to form a rectangle of length 3p cm. If p = 8, what was the breadth of the rectangle?
3 m
Image in this question is not available.
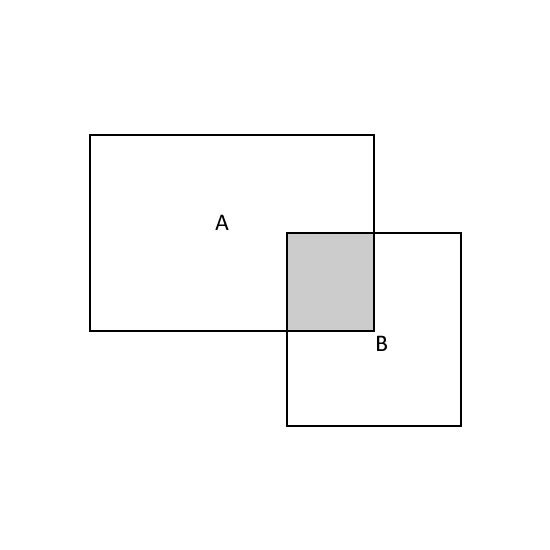
Level 2
Rectangle A and Rectangle B overlap each other. Given that 16 of Rectangle A is shaded while 14 of Rectangle B is shaded, what fraction of the figure is not shaded?
Level 2
Rectangle A and Rectangle B overlap each other. Given that 16 of Rectangle A is shaded while 14 of Rectangle B is shaded, what fraction of the figure is not shaded?
Image in this question is not available.
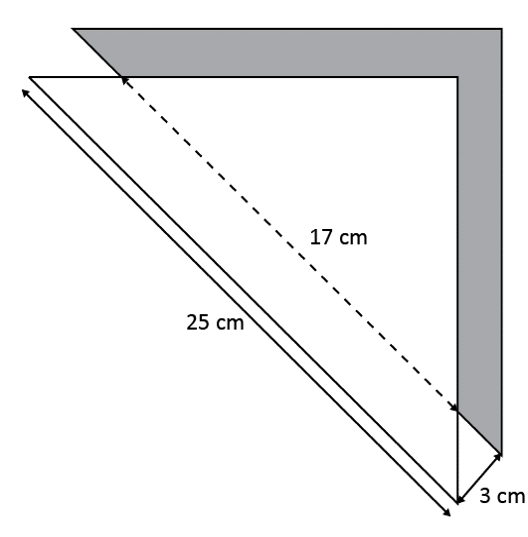
Level 3
Two identical right-angled triangles overlap each other as shown. Find the area of the shaded part.
Level 3
Two identical right-angled triangles overlap each other as shown. Find the area of the shaded part.
Image in this question is not available.
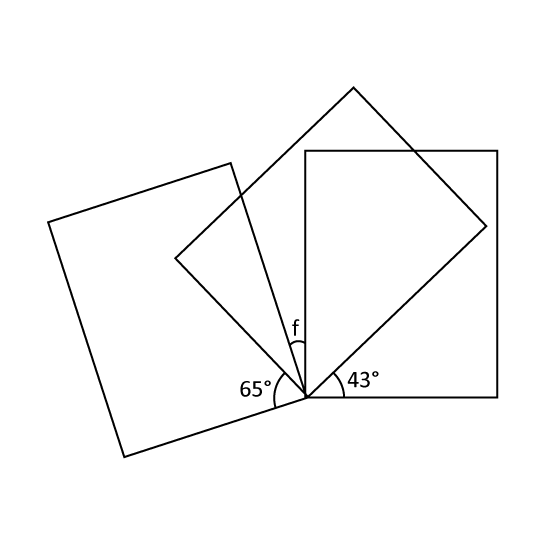
Level 2
The figure shows 3 rectangles. What is the value of ∠f?
Level 2
The figure shows 3 rectangles. What is the value of ∠f?
Image in this question is not available.
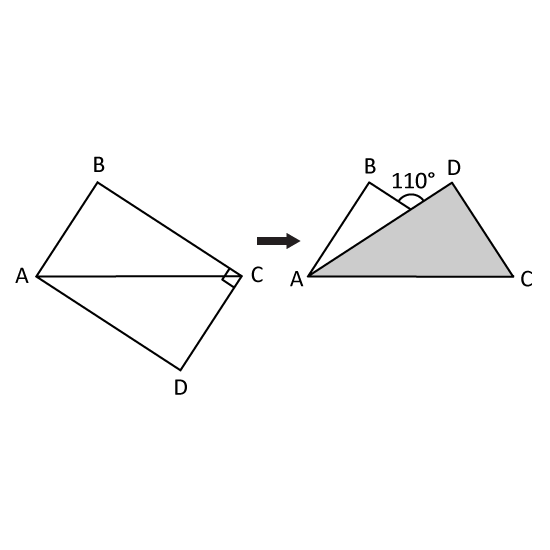
Level 3
Ben folded a rectangular piece of paper ABCD along its diagonal AC. Find ∠ACD.
Level 3
Ben folded a rectangular piece of paper ABCD along its diagonal AC. Find ∠ACD.
Image in this question is not available.
Level 3
A cuboid has a volume of 300 cm3. Its base is a rectangle which has a perimeter of 32 cm. The ratio of the length to the breadth of the rectangle is 5 : 3. Find its height.
3 m
Image in this question is not available.
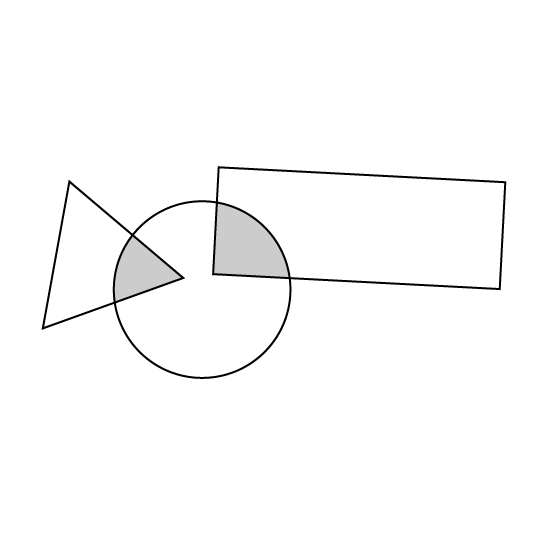
Level 3
The figure is not drawn to scale. The ratio of the area of the rectangle to the area of the circle to the area of the triangle is 21 : 17 : 4. If 14 of the triangle and 37 of the rectangle are shaded, what is the ratio of the total shaded area to the total of the unshaded area? Leave your answer in the simplest form.
Level 3
The figure is not drawn to scale. The ratio of the area of the rectangle to the area of the circle to the area of the triangle is 21 : 17 : 4. If 14 of the triangle and 37 of the rectangle are shaded, what is the ratio of the total shaded area to the total of the unshaded area? Leave your answer in the simplest form.
Image in this question is not available.
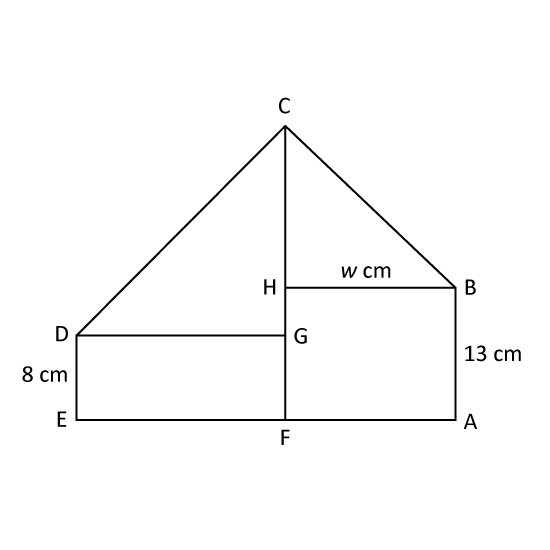
Level 3 PSLEThe figure is made up of two rectangles, ABHF and FGDE, and two right-angled isosceles triangles, BCH and DCG. BA = 13 cm, DE = 8 cm and BH = w cm. AFE and CHGF are straight lines.
- Find the length of AE in terms of w. Give your answer in the simplest form.
- Find the total area of the figure when w = 16.
Level 3 PSLEThe figure is made up of two rectangles, ABHF and FGDE, and two right-angled isosceles triangles, BCH and DCG. BA = 13 cm, DE = 8 cm and BH = w cm. AFE and CHGF are straight lines.
- Find the length of AE in terms of w. Give your answer in the simplest form.
- Find the total area of the figure when w = 16.
Image in this question is not available.
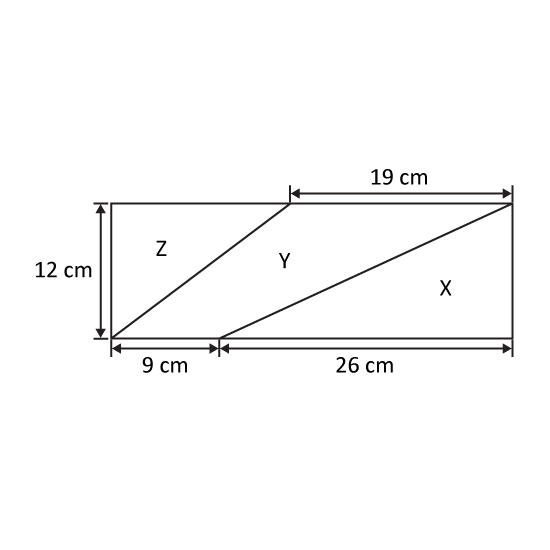
Level 3
The figure shows a rectangular piece of paper. It is cut into 3 parts, X, Y and Z. Find the ratio of the area of the rectangular piece of paper to the area of Y. Leave your answer in the simplest form.
Level 3
The figure shows a rectangular piece of paper. It is cut into 3 parts, X, Y and Z. Find the ratio of the area of the rectangular piece of paper to the area of Y. Leave your answer in the simplest form.
Image in this question is not available.
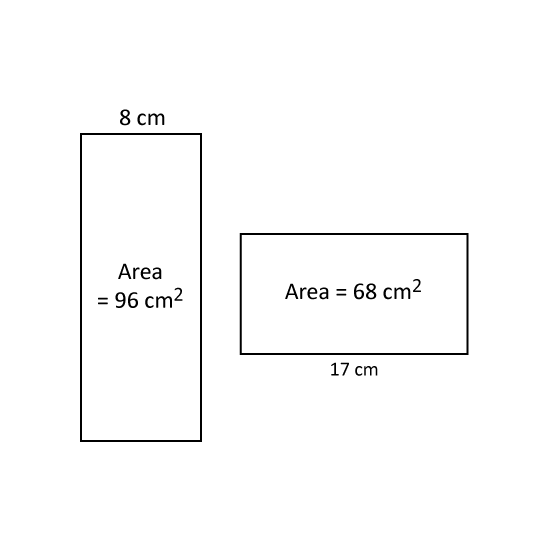
Level 3
Find the difference in perimeter between the 2 rectangles.
Level 3
Find the difference in perimeter between the 2 rectangles.
Image in this question is not available.