Level 3
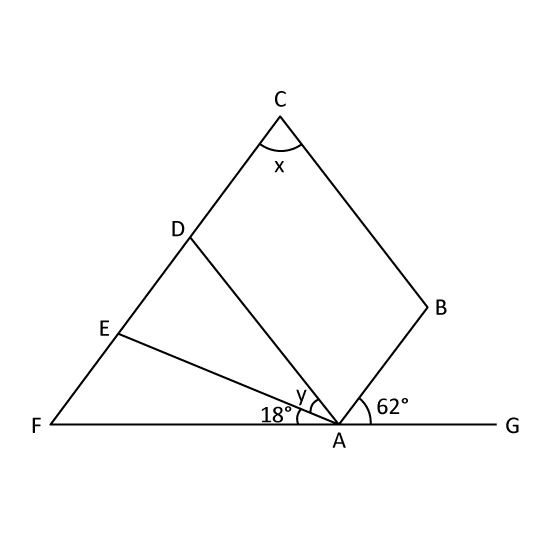
In the figure, ABCD is a parallelogram. CF, FG and AB are straight lines. ADE is an isosceles triangle.
- Find ∠x.
- Find ∠y.
Level 3
In the figure, ABCD is a parallelogram. CF, FG and AB are straight lines. ADE is an isosceles triangle.
- Find ∠x.
- Find ∠y.
Image in this question is not available.
Level 2
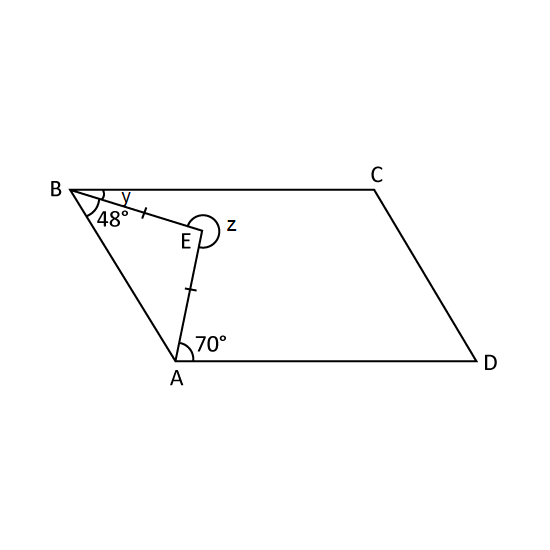
In the figure, ABCD is a parallelogram and EA = EB.
- Find ∠y.
- Find ∠z.
Level 2
In the figure, ABCD is a parallelogram and EA = EB.
- Find ∠y.
- Find ∠z.
Image in this question is not available.
Level 3
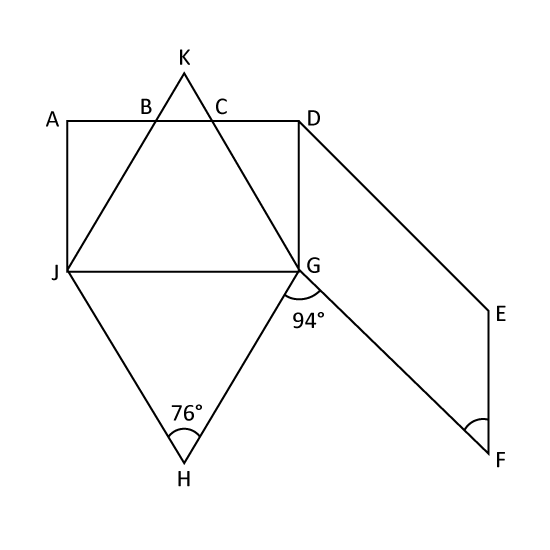
In the figure, ADGJ is a rectangle, GHJK is a rhombus and DEFG is a parallelogram. ∠GHJ = 76° and ∠FGH = 94°.
- Find ∠CGD.
- Find ∠GFE.
Level 3
In the figure, ADGJ is a rectangle, GHJK is a rhombus and DEFG is a parallelogram. ∠GHJ = 76° and ∠FGH = 94°.
- Find ∠CGD.
- Find ∠GFE.
Image in this question is not available.
Level 3
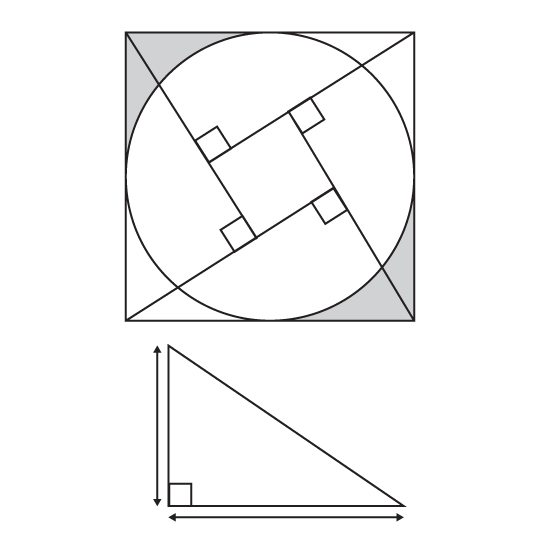
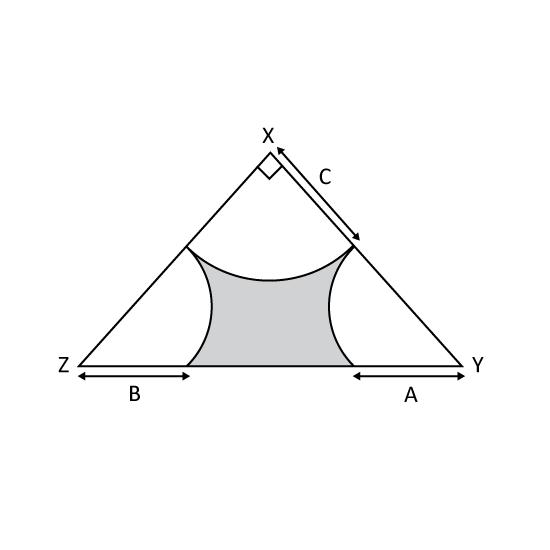
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Level 3
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Image in this question is not available.
Level 3
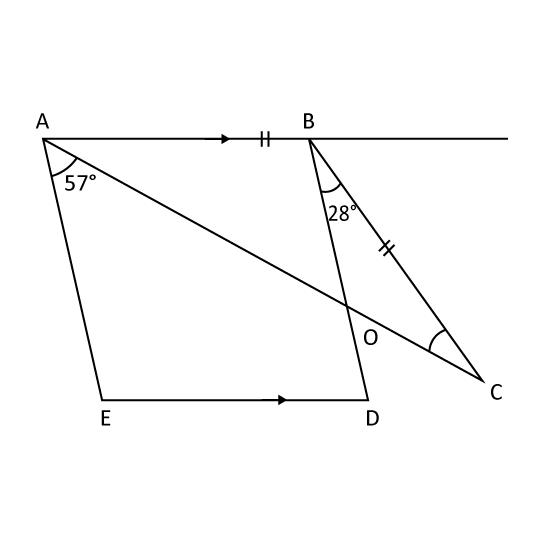
The figure is not drawn to scale. ABDE is a parallelogram.
∠EAO is 57° and ∠DBC is 28°. ABC is an isosceles triangle and AB = BC.
- Find ∠OCB.
- Find ∠AED.
Level 3
The figure is not drawn to scale. ABDE is a parallelogram.
∠EAO is 57° and ∠DBC is 28°. ABC is an isosceles triangle and AB = BC.
- Find ∠OCB.
- Find ∠AED.
Image in this question is not available.
Level 3
ABEF is a parallelogram. DF, DG, AF and BE are straight lines. AB = AG. Find ∠BGC.
Level 3
ABEF is a parallelogram. DF, DG, AF and BE are straight lines. AB = AG. Find ∠BGC.
Image in this question is not available.
Level 3
The figure is not drawn to scale. A, B and C are radii of 21 cm long. Find the area of the shaded part. (Take π = 227)
Level 3
The figure is not drawn to scale. A, B and C are radii of 21 cm long. Find the area of the shaded part. (Take π = 227)
Image in this question is not available.
Level 3
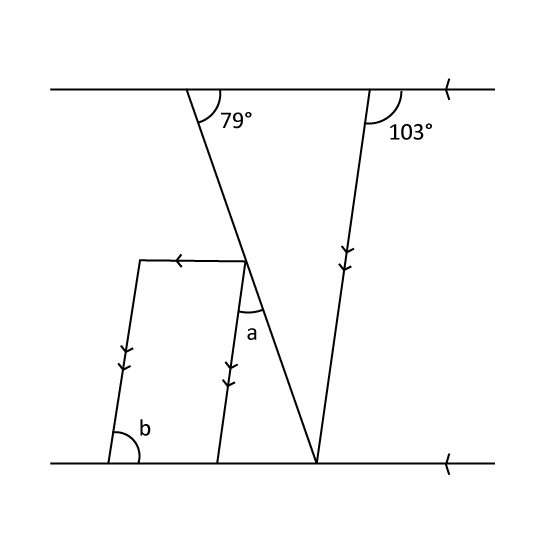
The figure is not drawn to scale. Find
- ∠a
- ∠b
Level 3
The figure is not drawn to scale. Find
- ∠a
- ∠b
Image in this question is not available.
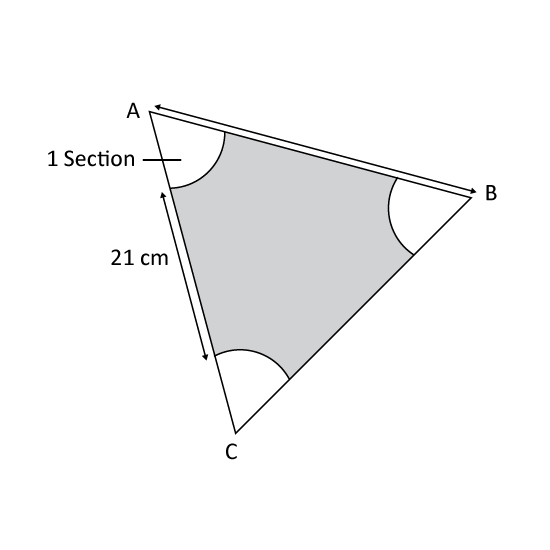
Level 3
Three similar sections are cut away from an equilateral cardboard triangle ABC. Each side of the equilateral triangle is 56 cm. Find the perimeter of the remaining cardboard. (Take π = 3.14)
Level 3
Three similar sections are cut away from an equilateral cardboard triangle ABC. Each side of the equilateral triangle is 56 cm. Find the perimeter of the remaining cardboard. (Take π = 3.14)
Image in this question is not available.
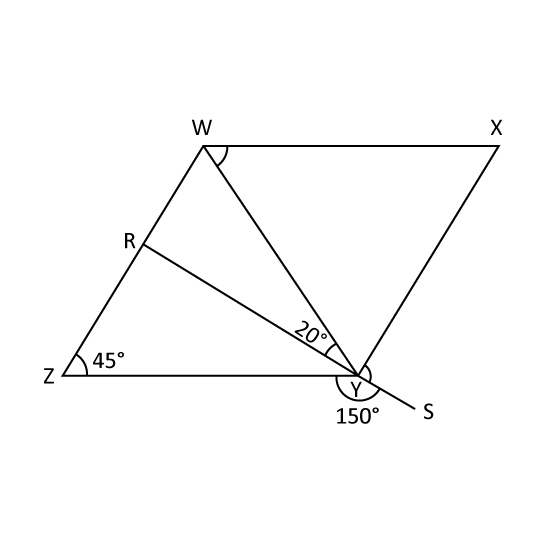
Level 3 PSLE
In the figure, WXYZ is a parallelogram. WRZ and RYS are straight lines. ∠SYZ = 150°, ∠WZY = 45° and ∠WYR = 20°.
- Find ∠XYS.
- Find ∠XWY.
Level 3 PSLE
In the figure, WXYZ is a parallelogram. WRZ and RYS are straight lines. ∠SYZ = 150°, ∠WZY = 45° and ∠WYR = 20°.
- Find ∠XYS.
- Find ∠XWY.
Image in this question is not available.
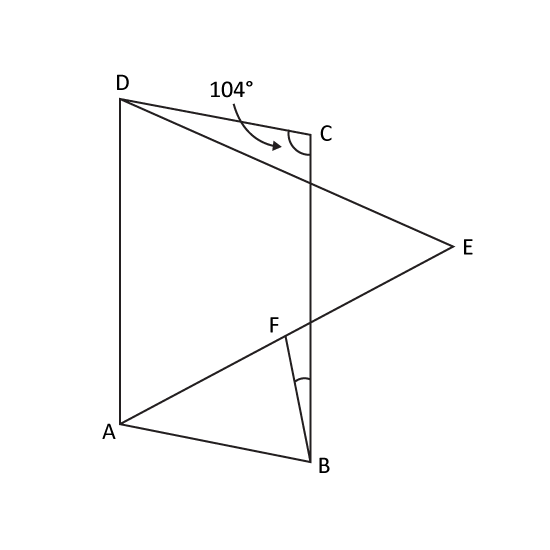
Level 3
In the figure, ABCD is a parallelogram with length AD twice the length of AB. ADE is an equilateral triangle. F is a point on AE such that AF = FE. ∠BCD is 104°. Find ∠FBC .
Level 3
In the figure, ABCD is a parallelogram with length AD twice the length of AB. ADE is an equilateral triangle. F is a point on AE such that AF = FE. ∠BCD is 104°. Find ∠FBC .
Image in this question is not available.
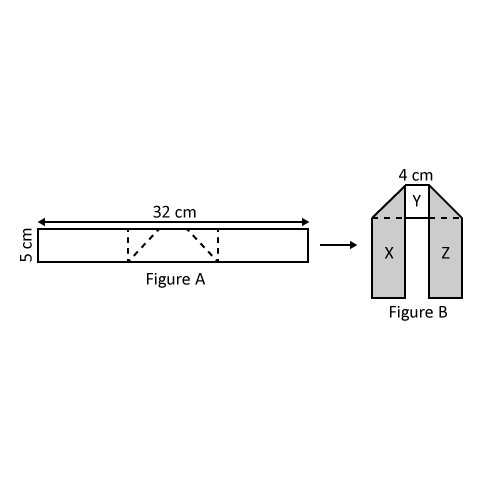
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Image in this question is not available.
Level 3
Ben has a white rectangular card which is grey on the other side. He folds the card along its diagonal ED. Find
(a) ∠a
(b) ∠b
(c) ∠c
Level 3
Ben has a white rectangular card which is grey on the other side. He folds the card along its diagonal ED. Find
(a) ∠a
(b) ∠b
(c) ∠c
Image in this question is not available.
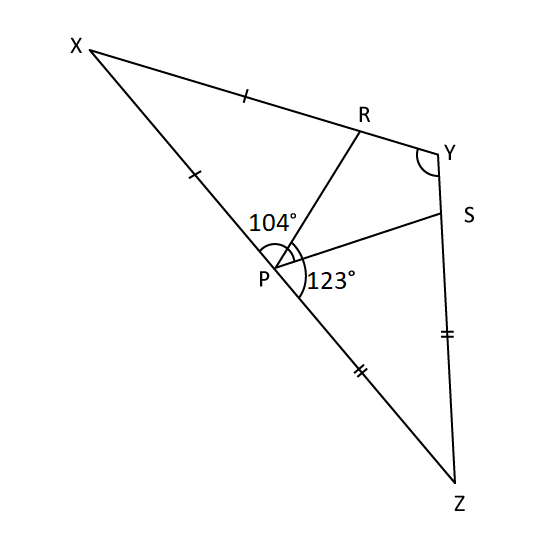
Level 3 PSLE
In the figure, XYZ is a triangle. P, R and S are points on the triangle such that XP = XR and SZ = PZ. If ∠XPR = 104°and ∠SPZ = 123°, find ∠RYS.
Level 3 PSLE
In the figure, XYZ is a triangle. P, R and S are points on the triangle such that XP = XR and SZ = PZ. If ∠XPR = 104°and ∠SPZ = 123°, find ∠RYS.
Image in this question is not available.
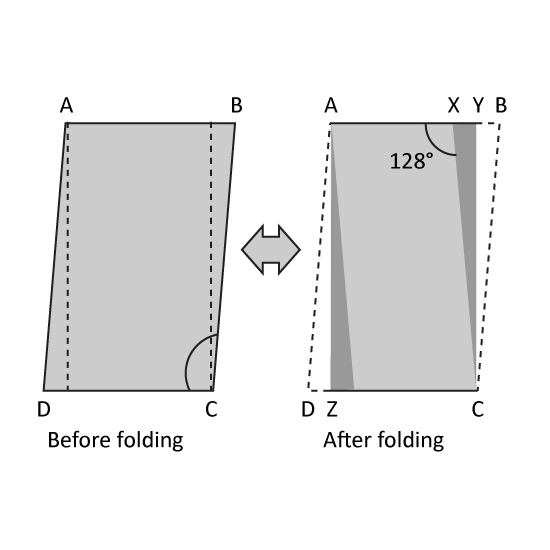
Level 3
ABCD is a parallelogram which was folded along the dotted lines to form rectangle AYCZ. The two shaded triangles are the flaps formed after the folding. Given that ∠AXC = 128°, find ∠DAB.
Level 3
ABCD is a parallelogram which was folded along the dotted lines to form rectangle AYCZ. The two shaded triangles are the flaps formed after the folding. Given that ∠AXC = 128°, find ∠DAB.
Image in this question is not available.
Level 3
In the figure, not drawn to scale, ABC, CDE, BFE, and AFD are straight lines. What is the value of ∠x + ∠y?
Level 3
In the figure, not drawn to scale, ABC, CDE, BFE, and AFD are straight lines. What is the value of ∠x + ∠y?
Image in this question is not available.
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Image in this question is not available.
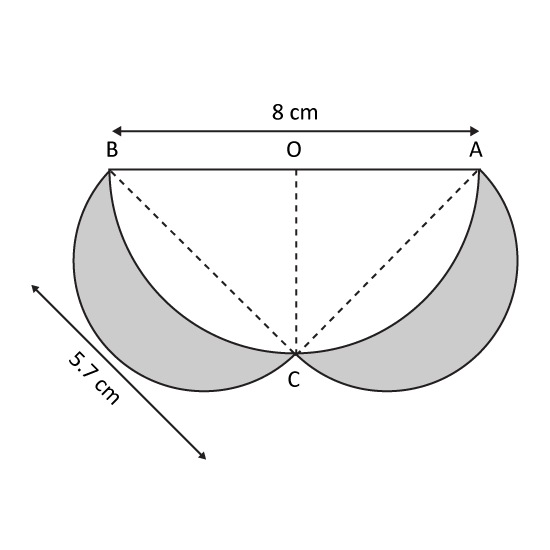
Level 3
The figure is made up of a big semicircle of diameter 8 cm and 2 small semicircles with diameter 5.7 cm. Find the shaded area. Round off the answer to nearest 1 decimal place. (Take π = 3.14)
Level 3
The figure is made up of a big semicircle of diameter 8 cm and 2 small semicircles with diameter 5.7 cm. Find the shaded area. Round off the answer to nearest 1 decimal place. (Take π = 3.14)
Image in this question is not available.
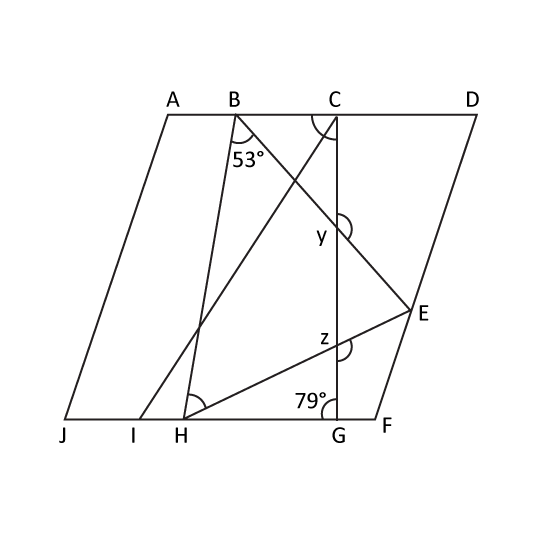
Level 3
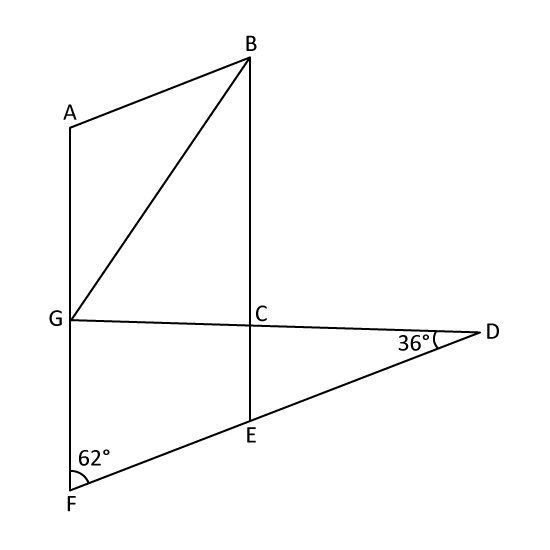
The figure is not drawn to scale. ADFJ is a parallelogram. CGI and BEH are triangles. ∠CGH = 79° and HBE = 53°. Find
- ∠BCG
- the sum of ∠BHE, ∠CYE and ∠EZG.
Level 3
The figure is not drawn to scale. ADFJ is a parallelogram. CGI and BEH are triangles. ∠CGH = 79° and HBE = 53°. Find
- ∠BCG
- the sum of ∠BHE, ∠CYE and ∠EZG.
Image in this question is not available.
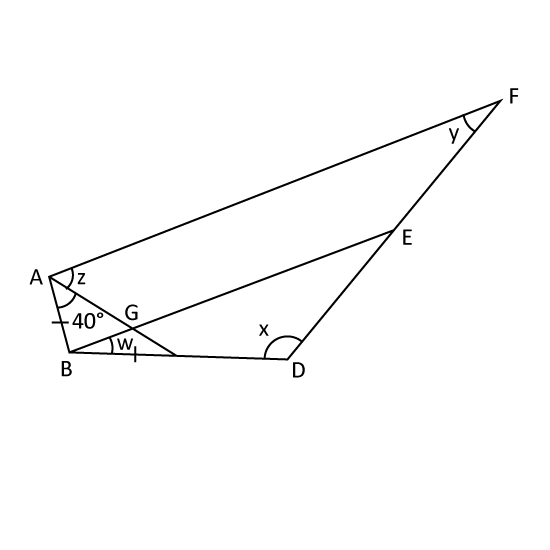
Level 3
The figure is not drawn to scale. ∠BAC = 40°, BA = BC and AF//BE. Given that ∠z is
12 of ∠x and ∠z is 3 times of ∠y, find
- ∠z
- ∠w.
Level 3
The figure is not drawn to scale. ∠BAC = 40°, BA = BC and AF//BE. Given that ∠z is
12 of ∠x and ∠z is 3 times of ∠y, find
- ∠z
- ∠w.
Image in this question is not available.