Level 2
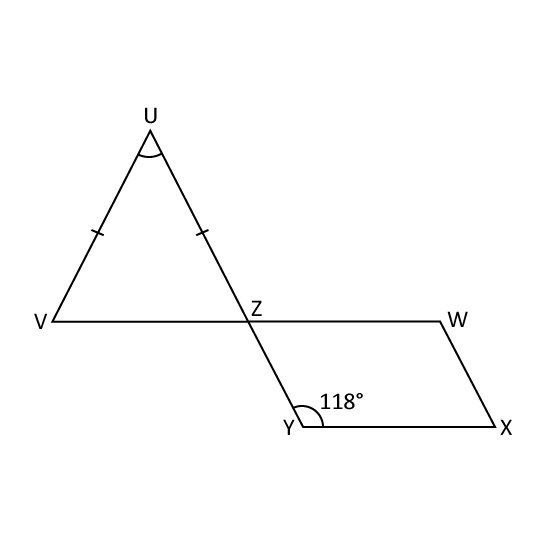
The figure shows a parallelogram WXVZ and an isosceles triangle UZV. WZV and UZV are straight lines. Given that ∠XYZ = 118°, what is the value of ∠ZUV?
Level 2
The figure shows a parallelogram WXVZ and an isosceles triangle UZV. WZV and UZV are straight lines. Given that ∠XYZ = 118°, what is the value of ∠ZUV?
Image in this question is not available.
Level 2
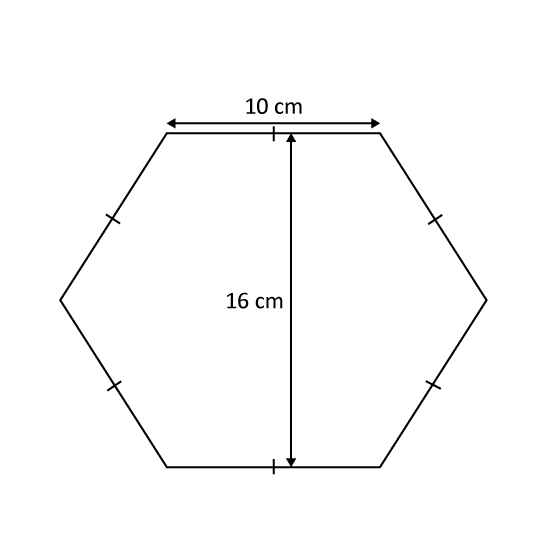
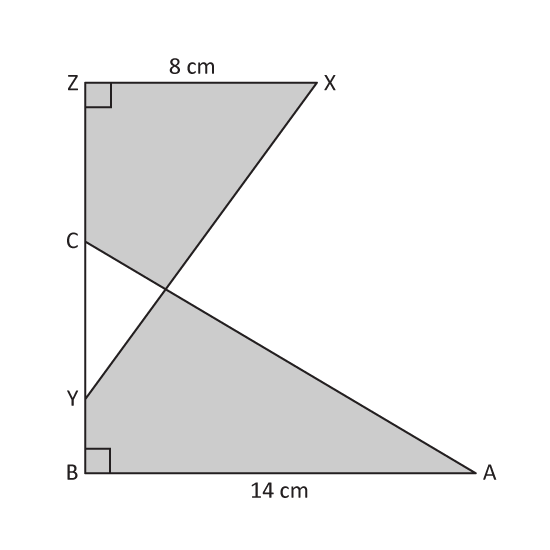
Find the area of the following figure which is made up of 6 identical triangles.
Level 2
Find the area of the following figure which is made up of 6 identical triangles.
Image in this question is not available.
Level 2
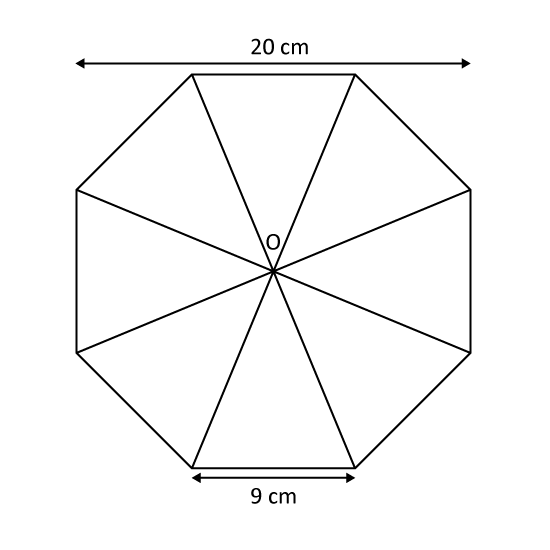
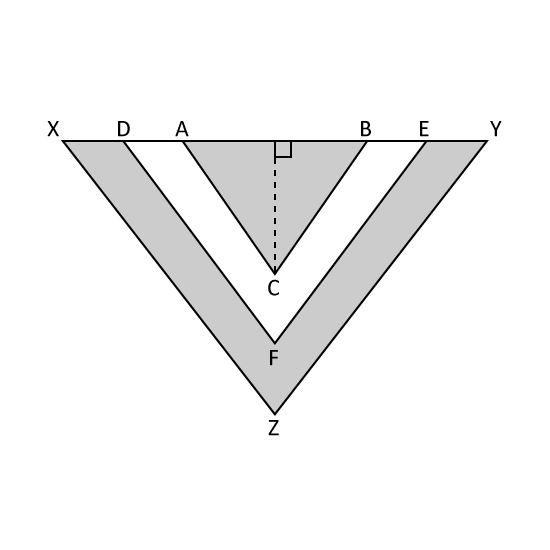
Find the area of the following figure which is made up of 8 identical triangles where O is the centre of the figure.
Level 2
Find the area of the following figure which is made up of 8 identical triangles where O is the centre of the figure.
Image in this question is not available.
Level 2
Tony drove a distance of 15 km in 10 minutes.
- What was his speed in km/h?
- How long will it take him to cover 360 km at this speed? Express the answer in hours.
3 m
Image in this question is not available.
Level 3 PSLE
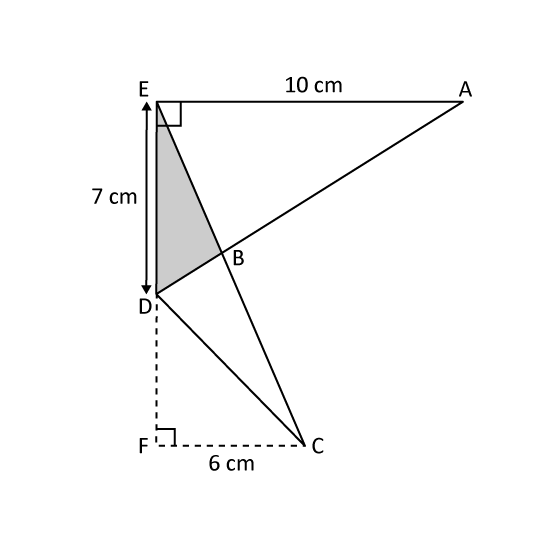
Figure ABCDE has an area of 42 cm2. ABD and CBE are straight lines. Find the area of the shaded triangle BDE.
Level 3 PSLE
Figure ABCDE has an area of 42 cm2. ABD and CBE are straight lines. Find the area of the shaded triangle BDE.
Image in this question is not available.
Level 2
A van covers a distance of 45 km in 25 minutes.
- At what speed is it travelling?
- How long will it take to cover a distance of 36 km?
3 m
Image in this question is not available.
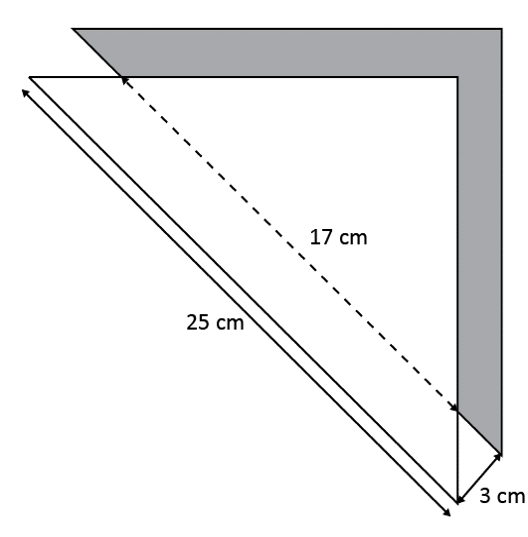
Level 3 PSLE
In the figure, ABC and XZY are identical right-angled triangles. The total area of the shaded parts is 96 cm2. Find the area of the unshaded part.
Level 3 PSLE
In the figure, ABC and XZY are identical right-angled triangles. The total area of the shaded parts is 96 cm2. Find the area of the unshaded part.
Image in this question is not available.
Level 2
The figure is made up of three triangles, ABC, XYZ and DEF not drawn to scale. The area of triangle XYZ is six times the area of triangle ABC. The area of triangle ABC is 13 of triangle DEF. The area of triangle ABC is 12 cm2. What is the total area of the shaded parts?
Level 2
The figure is made up of three triangles, ABC, XYZ and DEF not drawn to scale. The area of triangle XYZ is six times the area of triangle ABC. The area of triangle ABC is 13 of triangle DEF. The area of triangle ABC is 12 cm2. What is the total area of the shaded parts?
Image in this question is not available.
Level 2 PSLEJasmine had a piece of ribbon 17p cm long. She formed a triangle, with sides measuring p cm, 5p cm and 30 cm, with part of the wire.
- Express the length of the remaining ribbon in terms of p in the simplest form.
- Jasmine used the remaining ribbon to form a rectangle of length 3p cm. If p = 8, what was the breadth of the rectangle?
3 m
Image in this question is not available.
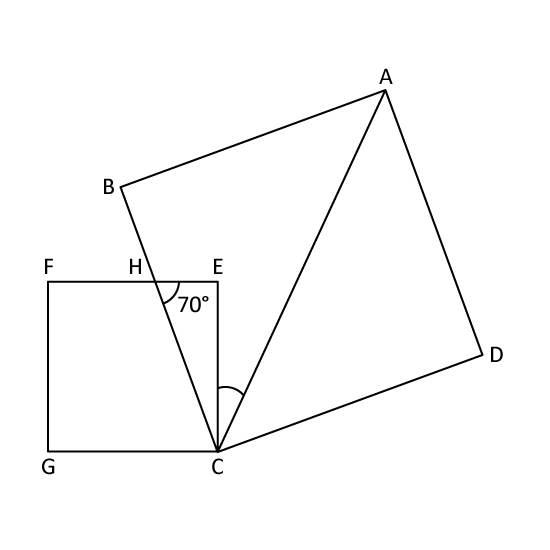
Level 2
ABCD and EFGC are different squares. Given that ∠EHC = 70°, find ∠ACE.
Level 2
ABCD and EFGC are different squares. Given that ∠EHC = 70°, find ∠ACE.
Image in this question is not available.
Level 3
In the figure, ABC and ADE are right-angled isosceles triangles. BD = CE = 2 cm. The shaded area is 22 cm2. Find the length of AC.
Level 3
In the figure, ABC and ADE are right-angled isosceles triangles. BD = CE = 2 cm. The shaded area is 22 cm2. Find the length of AC.
Image in this question is not available.
Level 3
Two identical right-angled triangles overlap each other as shown. Find the area of the shaded part.
Level 3
Two identical right-angled triangles overlap each other as shown. Find the area of the shaded part.
Image in this question is not available.
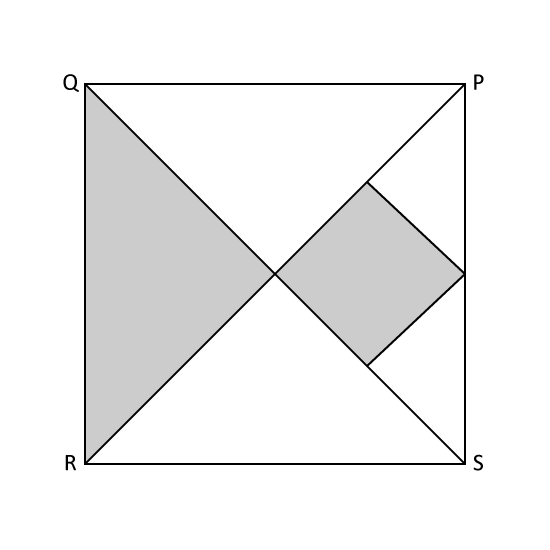
Level 2
Figure PQRS is a square. It is made up of 1 small square, 2 small triangles and 3 large triangles. PR and OS are straight lines. What fraction of the square PQRS is shaded?
Level 2
Figure PQRS is a square. It is made up of 1 small square, 2 small triangles and 3 large triangles. PR and OS are straight lines. What fraction of the square PQRS is shaded?
Image in this question is not available.
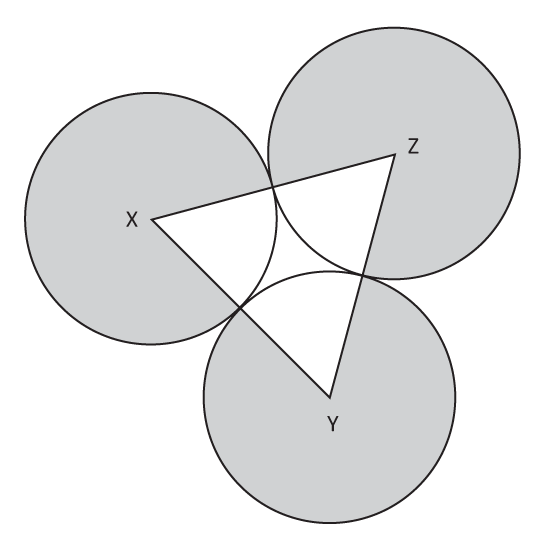
Level 2
X, Y and Z are centres of three identical circles. The length of XY is 7.2 m. XY, YZ and XZ are equal in length. Find the shaded area of the figure. (Take π = 3.14) Correct to 2 decimal places.
Level 2
X, Y and Z are centres of three identical circles. The length of XY is 7.2 m. XY, YZ and XZ are equal in length. Find the shaded area of the figure. (Take π = 3.14) Correct to 2 decimal places.
Image in this question is not available.
Level 3
Sam took 2 hours to walk from Building A to Building B which was 6 km away. On his way back from Building B to Building A, he increased his average walking speed by 1 km/h. How long did he take for his journey back?
3 m
Image in this question is not available.
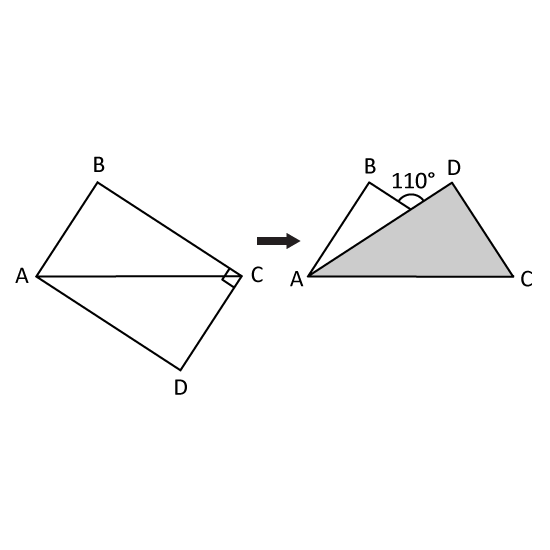
Level 3
Ben folded a rectangular piece of paper ABCD along its diagonal AC. Find ∠ACD.
Level 3
Ben folded a rectangular piece of paper ABCD along its diagonal AC. Find ∠ACD.
Image in this question is not available.
Level 3
Jake walks to school at an average speed of 4 km/h every day. One day, after walking a distance of 1 km, he realised that his watch was slow. So, he ran at a constant speed and managed to reach his school just on time. Later, he calculated that if he had run at this speed right from the start of the journey, he would have reached his school 5 minutes earlier. What was his running speed?
3 m
Image in this question is not available.
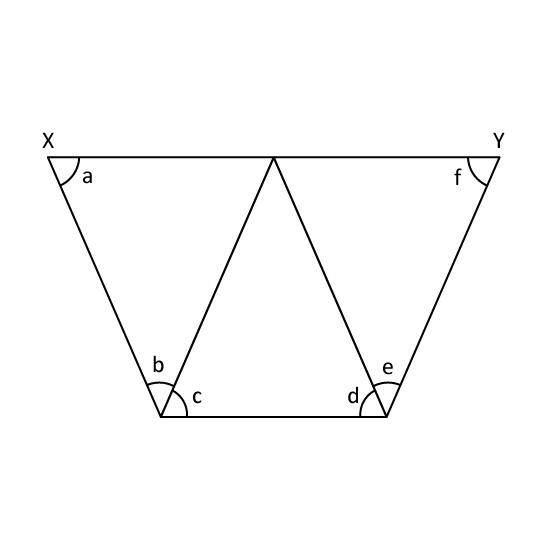
Level 2
The figure consists of 3 identical triangle. XY is a straight line. What is the sum of ∠a, ∠b, ∠c, ∠d, ∠e and ∠f?
Level 2
The figure consists of 3 identical triangle. XY is a straight line. What is the sum of ∠a, ∠b, ∠c, ∠d, ∠e and ∠f?
Image in this question is not available.
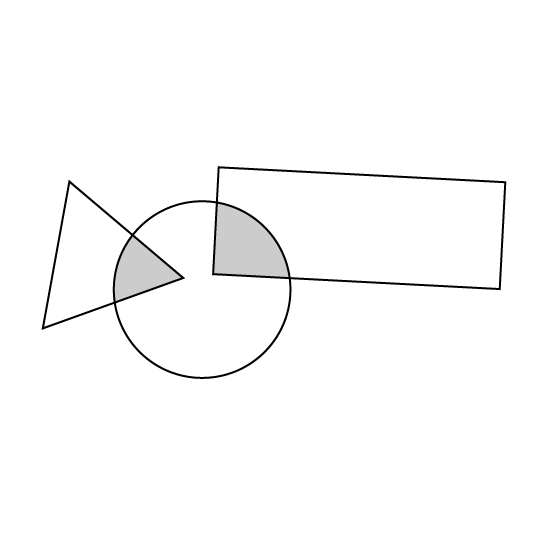
Level 3
The figure is not drawn to scale. The ratio of the area of the rectangle to the area of the circle to the area of the triangle is 21 : 17 : 4. If 14 of the triangle and 37 of the rectangle are shaded, what is the ratio of the total shaded area to the total of the unshaded area? Leave your answer in the simplest form.
Level 3
The figure is not drawn to scale. The ratio of the area of the rectangle to the area of the circle to the area of the triangle is 21 : 17 : 4. If 14 of the triangle and 37 of the rectangle are shaded, what is the ratio of the total shaded area to the total of the unshaded area? Leave your answer in the simplest form.
Image in this question is not available.
Level 3 PSLE
Peter and Justin ran in a race around a 400 m track. Peter ran at a speed of 190 m/min and Justin at a speed that was 25 m/min slower than Peter throughout the race. How many complete rounds would Peter have finished when he had run a distance of 300 m more than Justin?
3 m
Image in this question is not available.