Level 3 PSLE
Esther and Margi took part in a cycling race. Esther cycled at a speed of 20 km/h. Both of them did not change their speed throughout the race. When Margi covered 12 the distance, Esther was 3.5 km in front of her. Esther reached the finishing line at 10.45 a.m. What time did Margi reach the finishing line?
3 m
Image in this question is not available.
Level 3 PSLE
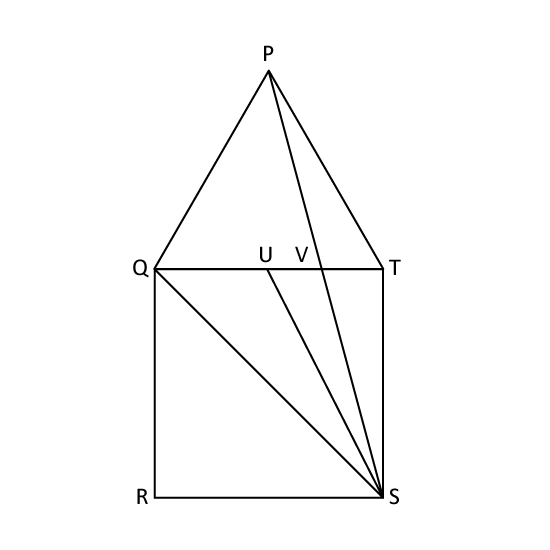
In the figure, QRST is a square and QPT is an equilateral triangle. Given that USV is 12°, find ∠QSU.
Level 3 PSLE
In the figure, QRST is a square and QPT is an equilateral triangle. Given that USV is 12°, find ∠QSU.
Image in this question is not available.
Level 3
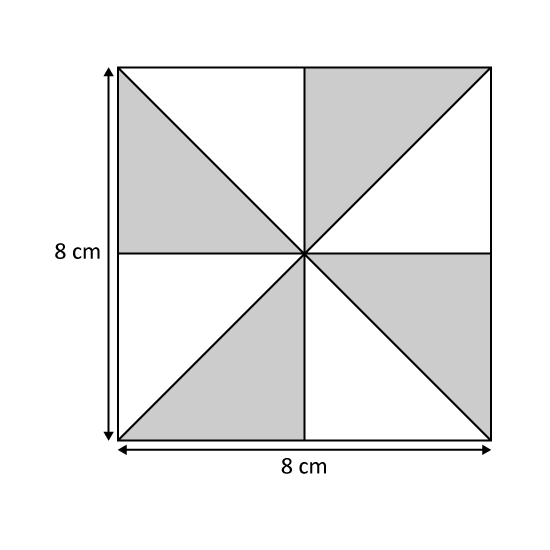
What is the total area of the shaded parts in the figure?
Level 3
What is the total area of the shaded parts in the figure?
Image in this question is not available.
Level 3
A bus and a car started travelling from Town A to Town B at the same time. After 5 hours, the car reached Town B while the bus covered only 710 of the journey. The speed of the car was 21 km/h more than the speed of the bus. Find the speed of the bus.
3 m
Image in this question is not available.
Level 3
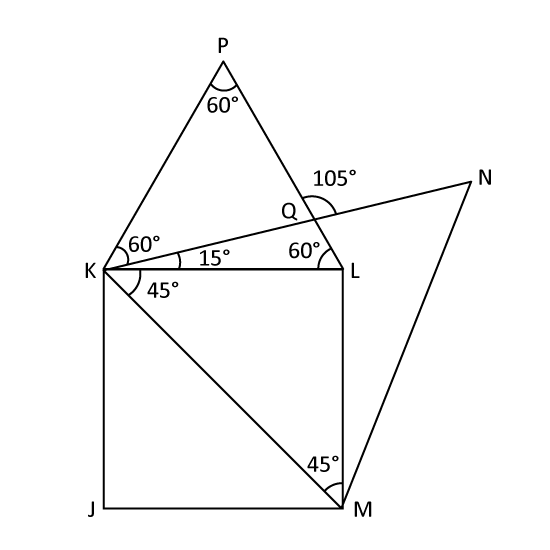
In the figure, not drawn to scale, JKLM is a square. PKL is an equilateral triangle. What is ∠PQN?
Level 3
In the figure, not drawn to scale, JKLM is a square. PKL is an equilateral triangle. What is ∠PQN?
Image in this question is not available.
Level 3
Jen and David started running together along a cross country track. When David completed the track in 40 minutes, Jen had run only
58 of the track. Jen’s average speed was 75 m/min slower than David’s.
- How long was the cross country track in m?
- Find Jen’s average speed in m/min.
3 m
Image in this question is not available.
Level 3 PSLE
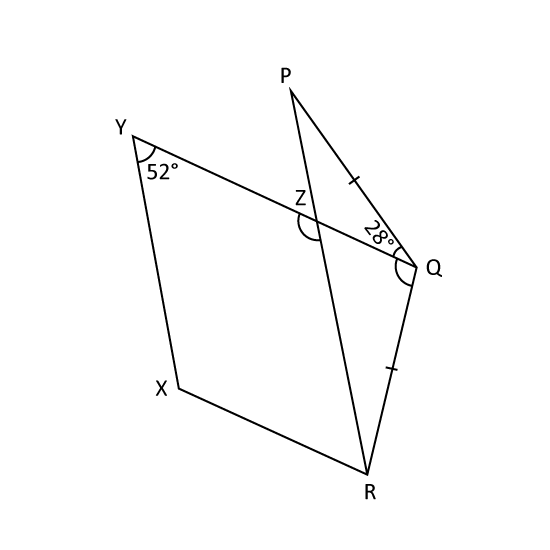
In the figure, RXYZ is a parallelogram. PZR and QZY are straight lines and PQ = QR. ∠PQZ = 28° and ∠XYZ = 52°.
- Find ∠YZR.
- Find ∠ZQR.
Level 3 PSLE
In the figure, RXYZ is a parallelogram. PZR and QZY are straight lines and PQ = QR. ∠PQZ = 28° and ∠XYZ = 52°.
- Find ∠YZR.
- Find ∠ZQR.
Image in this question is not available.
Level 3
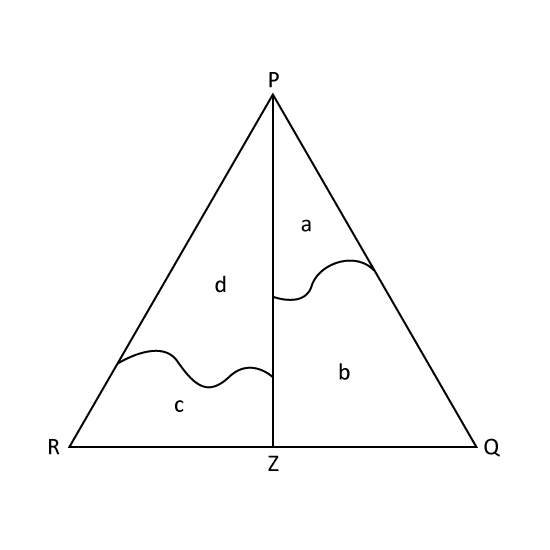
The figure shows the Triangle PQR that is divided into 4 parts a, b, c and d. The line PZ divides the triangle into 2 equal parts. The ratio of Area a to Area b is 1 : 3 and the ratio of Area b to Area c is 5 : 2. Area d is 210 cm2. What is the area of Triangle PQR?
Level 3
The figure shows the Triangle PQR that is divided into 4 parts a, b, c and d. The line PZ divides the triangle into 2 equal parts. The ratio of Area a to Area b is 1 : 3 and the ratio of Area b to Area c is 5 : 2. Area d is 210 cm2. What is the area of Triangle PQR?
Image in this question is not available.
Level 3 PSLE
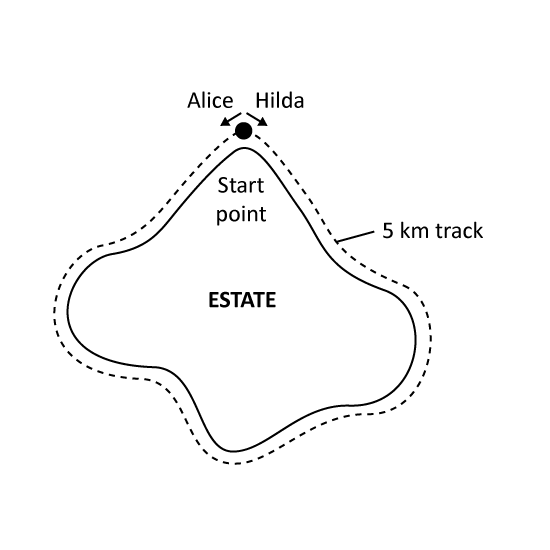
Alice and Hilda started jogging from the same point of a 5 km track round a housing estate. They started at the same time but in opposite directions. Alice jogged past Hilda after 2 km. Both of them did not change their speeds throughout. Alice took 30 min to complete one round. What was Hilda's jogging speed in m/min?
Level 3 PSLE
Alice and Hilda started jogging from the same point of a 5 km track round a housing estate. They started at the same time but in opposite directions. Alice jogged past Hilda after 2 km. Both of them did not change their speeds throughout. Alice took 30 min to complete one round. What was Hilda's jogging speed in m/min?
Image in this question is not available.
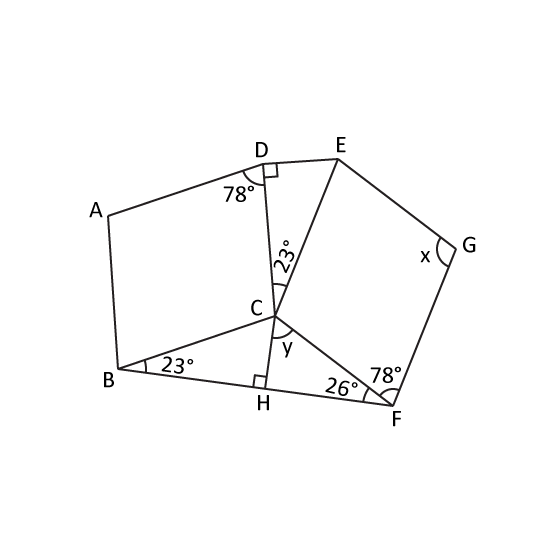
Level 3 PSLE ABCD and CFGE are identical parallelograms. HCB and EDC are identical right-angled triangles.
- Find ∠x.
- Find ∠y.
- Select the words that describe BHF in the statement:
BHF (is/is not) a straight line because the sum of angles BHC and CHF (is/is not) 180° Give your answers in this format. (Eg is, is not)
Level 3 PSLE ABCD and CFGE are identical parallelograms. HCB and EDC are identical right-angled triangles.
- Find ∠x.
- Find ∠y.
- Select the words that describe BHF in the statement:
BHF (is/is not) a straight line because the sum of angles BHC and CHF (is/is not) 180° Give your answers in this format. (Eg is, is not)
Image in this question is not available.
Level 3
At 7 a.m., a black car and a green car left the office and travelled at average speeds in opposite directions round a 25-km route. The black car took 15 minutes to complete each round while the green car took 20 minutes.
- Find the speed of the black car.
- Find the speed of the green car.
- If the 2 cars travelled without any interval of rest, at what time would the 2 cars next meet again at the office?
3 m
Image in this question is not available.
Level 3
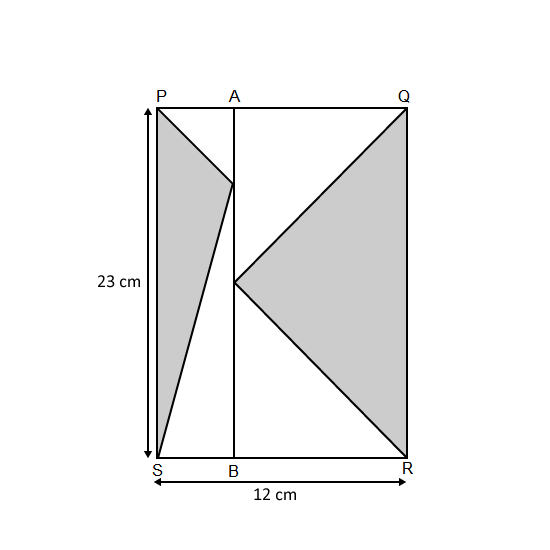
PQRS, PABS and ABRQ are rectangles. AQ is twice as long as AP. Find the area of the shaded parts.
Level 3
PQRS, PABS and ABRQ are rectangles. AQ is twice as long as AP. Find the area of the shaded parts.
Image in this question is not available.
Level 3
Vivian and Kyle started cycling at uniform speeds from the same place in opposite direction round an 800-m forest trail. Vivian took 40 seconds to complete each round while Kyle took 50 seconds.
- Find the distance covered per second by Vivian in m.
- Find the distance covered per second by Kyle in m.
- When the two cyclists next met again at the starting point, how far would Vivian have covered? Express the answer in km.
3 m
Image in this question is not available.
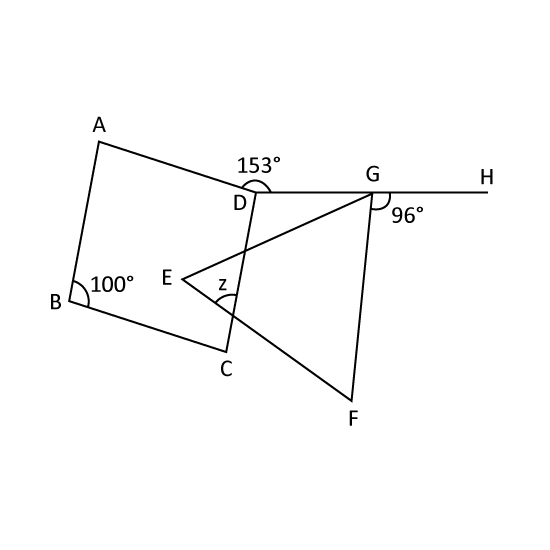
Level 3 PSLE
EFG is an equilateral triangle and ABCD is a rhombus. DGH is a straight line. Find ∠z.
Level 3 PSLE
EFG is an equilateral triangle and ABCD is a rhombus. DGH is a straight line. Find ∠z.
Image in this question is not available.
Level 3
Bus X and Bus Y left the same bus station at uniform speeds in the same direction round a 48-km circular route. Bus X took 45 minutes to complete each round while Bus Y took 30 minutes.
- How long would it take Bus Y to meet Bus Y for the first time? Express the answer in mixed number of hours.
- How far would Bus X be behind Bus Y after 12 hour?
3 m
Image in this question is not available.
Level 3 PSLE ABCD and BDEF are rhombuses. CGD is a straight line.
- Find ∠DBG.
- Find ∠CDE.
Level 3 PSLE ABCD and BDEF are rhombuses. CGD is a straight line.
- Find ∠DBG.
- Find ∠CDE.
Image in this question is not available.
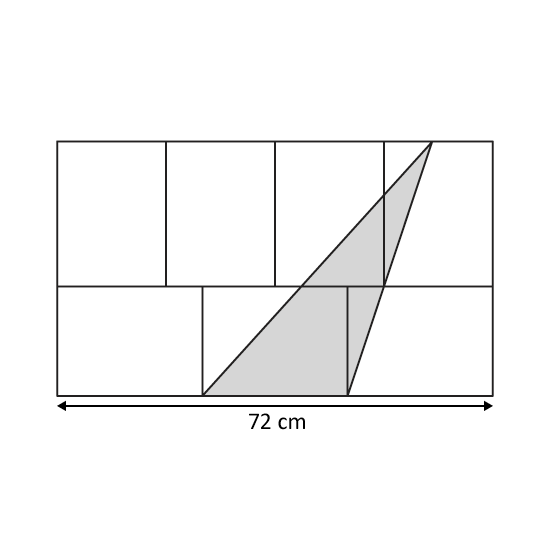
Level 3
The figure is made up of 7 identical rectangles.
- Find the perimeter of the figure.
- Find the shaded area.
Level 3
The figure is made up of 7 identical rectangles.
- Find the perimeter of the figure.
- Find the shaded area.
Image in this question is not available.
Level 3
Helen and Jomarie started off from the same place and drove at uniform speeds in the same direction round a 40-km circular racing track. Helen completed each round in 40 minutes. Jomarie took 50 minutes to complete each round.
- How far would Jomarie be behind Helen after 1 hour?
- How long after they started would it take Helen to meet Jomarie for the first time?
3 m
Image in this question is not available.
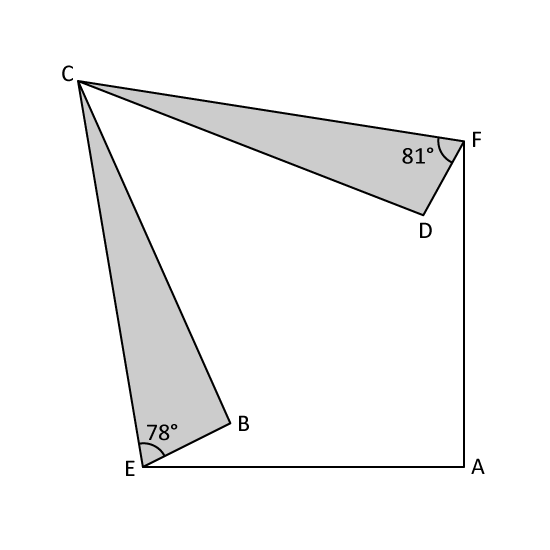
Level 3
The figure shows a piece of square paper ABCD folded at two of its corners B and D. Given that ∠CFD = 81° and ∠BEC = 78°, find ∠BCD.
Level 3
The figure shows a piece of square paper ABCD folded at two of its corners B and D. Given that ∠CFD = 81° and ∠BEC = 78°, find ∠BCD.
Image in this question is not available.
TRY FOR FREE
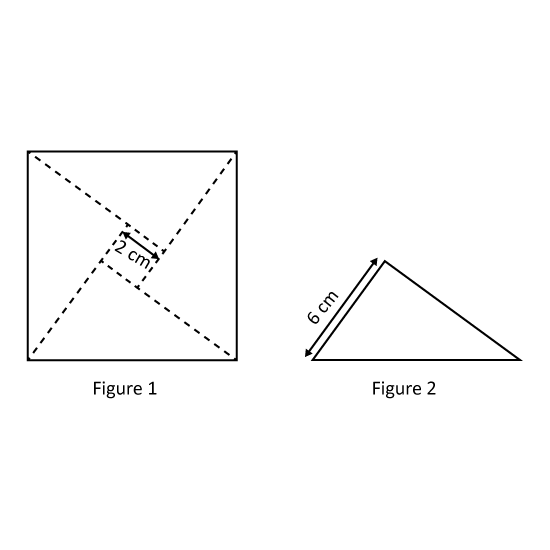
Level 3
Peter had a square piece of paper. He cut it along the dotted lines as shown in Figure 1 to get one small square of side 2 cm and four identical right-angled triangles. One such triangle is shown in Figure 2. Find the perimeter of the square piece of paper in Figure 1 before it was cut.
Level 3
Peter had a square piece of paper. He cut it along the dotted lines as shown in Figure 1 to get one small square of side 2 cm and four identical right-angled triangles. One such triangle is shown in Figure 2. Find the perimeter of the square piece of paper in Figure 1 before it was cut.
Image in this question is not available.