Level 3
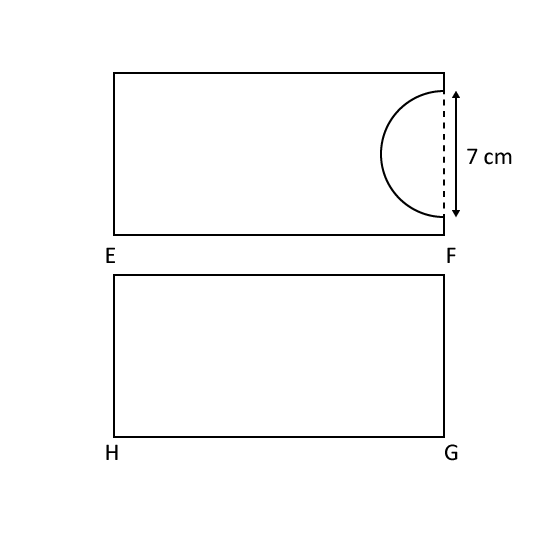
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Level 3
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Image in this question is not available.
Level 3 PSLE
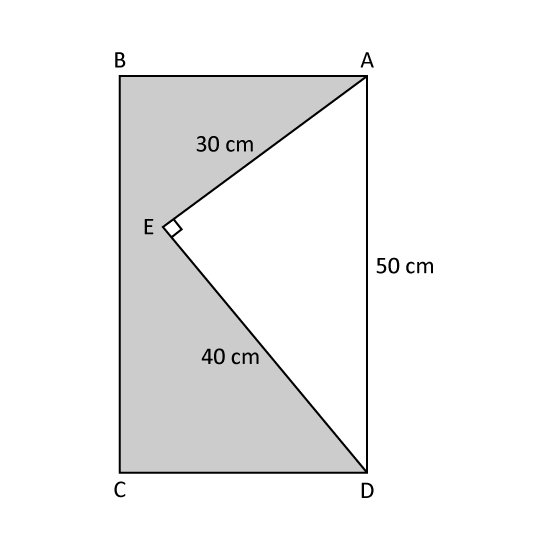
In the figure, ABCD is a rectangle and AED is a right-angled triangle with sides measuring 30 cm, 40 cm and 50 cm. The perimeter of the shaded part is 176 cm. What is the ratio of the area of the triangle to the area of the shaded part? Give your answer in the simplest form.
Level 3 PSLE
In the figure, ABCD is a rectangle and AED is a right-angled triangle with sides measuring 30 cm, 40 cm and 50 cm. The perimeter of the shaded part is 176 cm. What is the ratio of the area of the triangle to the area of the shaded part? Give your answer in the simplest form.
Image in this question is not available.
Level 3 PSLE
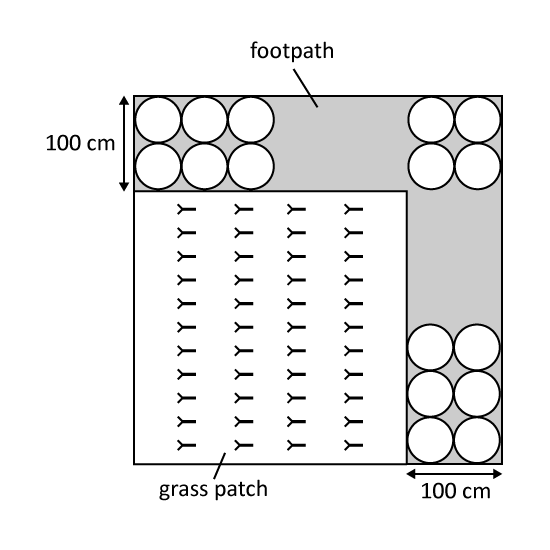
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Level 3 PSLE
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Image in this question is not available.
Level 3
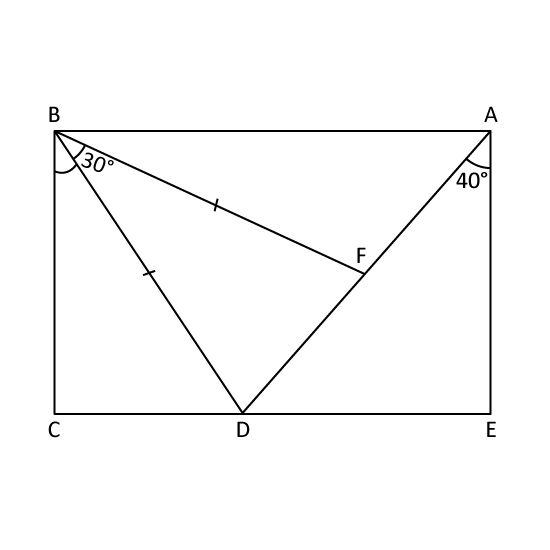
ABCE is a rectangle. Given that FBD is an isosceles triangle, find ∠DBC.
Level 3
ABCE is a rectangle. Given that FBD is an isosceles triangle, find ∠DBC.
Image in this question is not available.
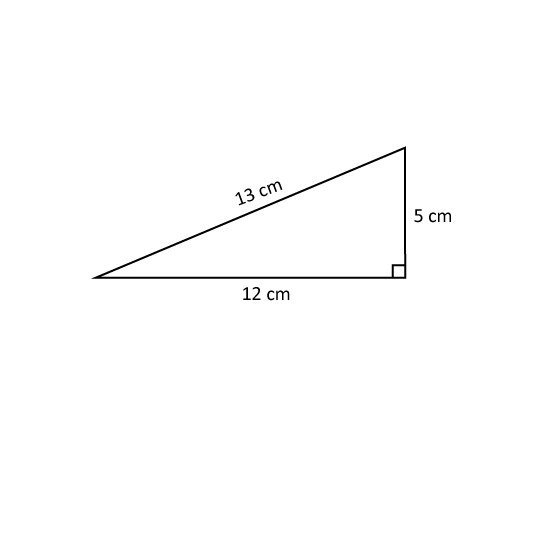
Level 3 PSLE The figure shows a right-angled triangle.
- Find the area of the triangle.
- Bruce wants to cut such triangles from a rectangular piece of cardboard 50 cm by 80 cm. At most, how many of such triangles can he cut?
Level 3 PSLE The figure shows a right-angled triangle.
- Find the area of the triangle.
- Bruce wants to cut such triangles from a rectangular piece of cardboard 50 cm by 80 cm. At most, how many of such triangles can he cut?
Image in this question is not available.
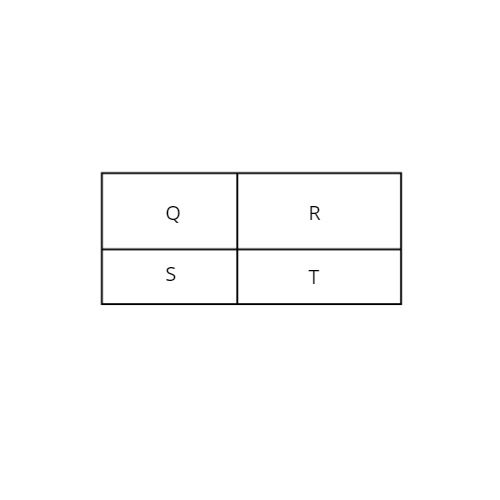
Level 3
The figure shows four rectangles Q, R, S and T not drawn to scale. The areas of rectangles Q, R and S are 30 cm22, 40 cm22 and 24 cm22 respectively. What is the area of rectangle T?
Level 3
The figure shows four rectangles Q, R, S and T not drawn to scale. The areas of rectangles Q, R and S are 30 cm22, 40 cm22 and 24 cm22 respectively. What is the area of rectangle T?
Image in this question is not available.
Level 3
In the figure not drawn to scale, 4 identical rectangles were placed around square ABCD to form a larger square, EFGH. The area of one rectangle is 12 cm2, and the area of ABCD is 14 of EFGH. Find the length of one rectangle.
Level 3
In the figure not drawn to scale, 4 identical rectangles were placed around square ABCD to form a larger square, EFGH. The area of one rectangle is 12 cm2, and the area of ABCD is 14 of EFGH. Find the length of one rectangle.
Image in this question is not available.
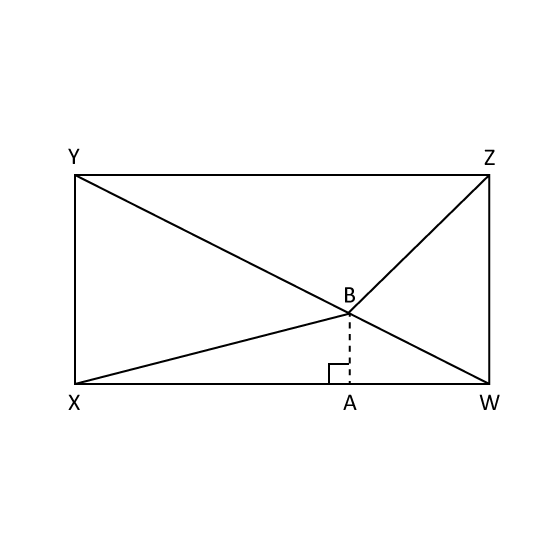
Level 3
The figure shows a rectangle WXYZ. The lines are extended from point W, X, Y and Z and they meet at point B. The length of YZ is 30 cm. Given that the area of triangle WBZ is 65 cm2 and the area of triangle XBY is 105 cm2, find the breadth of the rectangle in mixed number.
Level 3
The figure shows a rectangle WXYZ. The lines are extended from point W, X, Y and Z and they meet at point B. The length of YZ is 30 cm. Given that the area of triangle WBZ is 65 cm2 and the area of triangle XBY is 105 cm2, find the breadth of the rectangle in mixed number.
Image in this question is not available.
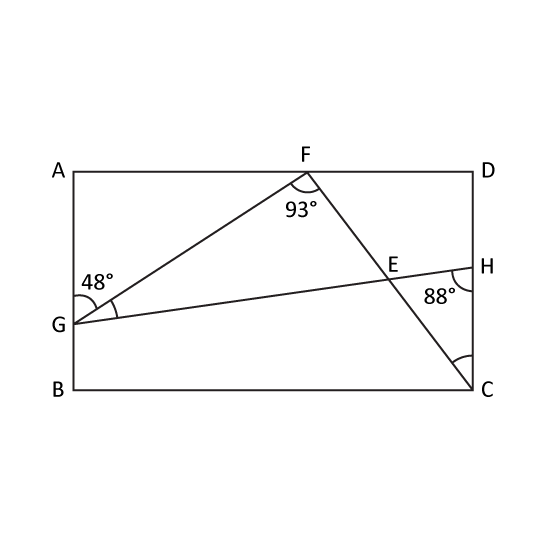
Level 3 PSLEIn the figure, ABCD is a rectangle. The points F, G, and H lie on the rectangle ABCD. CEF and HEG are straight lines.
- Find ∠FGH.
- Find ∠ECH.
Level 3 PSLEIn the figure, ABCD is a rectangle. The points F, G, and H lie on the rectangle ABCD. CEF and HEG are straight lines.
- Find ∠FGH.
- Find ∠ECH.
Image in this question is not available.
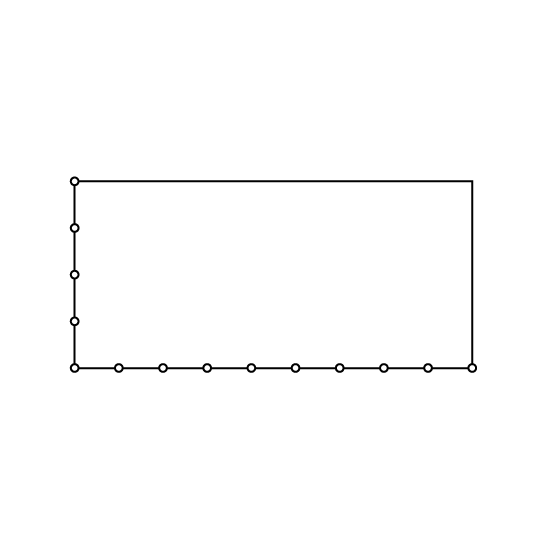
Level 3
5 poles are placed along the breadth of a rectangular field. The space between 2 poles is 50 m. If 10 poles are placed along the length of the rectangular field in the similar way, what is the perimeter of the rectangle? Give the answer in meters.
Level 3
5 poles are placed along the breadth of a rectangular field. The space between 2 poles is 50 m. If 10 poles are placed along the length of the rectangular field in the similar way, what is the perimeter of the rectangle? Give the answer in meters.
Image in this question is not available.
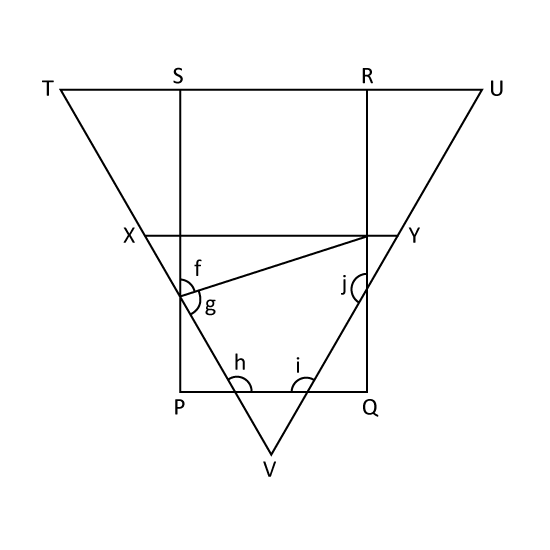
Level 3
VXY is an equilateral triangle, PQRS is a rectangle and TUYX is a trapezium. VXT and VYU are straight lines. If ∠f = 80°, find
- ∠XTU
- Sum of ∠g, ∠h, ∠i and ∠j.
Level 3
VXY is an equilateral triangle, PQRS is a rectangle and TUYX is a trapezium. VXT and VYU are straight lines. If ∠f = 80°, find
- ∠XTU
- Sum of ∠g, ∠h, ∠i and ∠j.
Image in this question is not available.
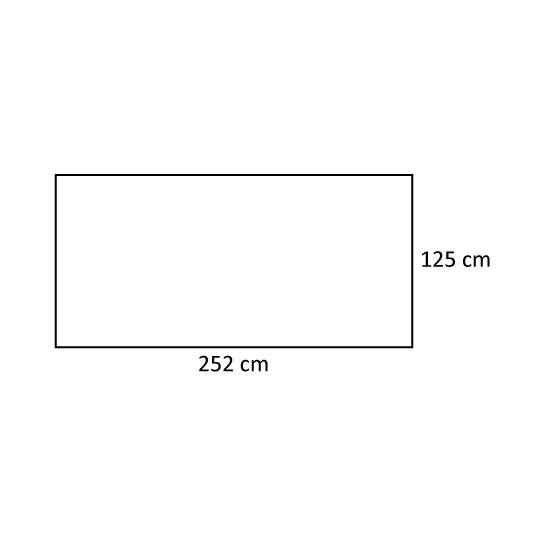
Level 3
A room has dimensions 252 cm by 125 cm. Tiles with dimension 20 cm by 12 cm were arranged on the floor. What is the maximum number of complete tiles that can be placed on the floor?
Level 3
A room has dimensions 252 cm by 125 cm. Tiles with dimension 20 cm by 12 cm were arranged on the floor. What is the maximum number of complete tiles that can be placed on the floor?
Image in this question is not available.
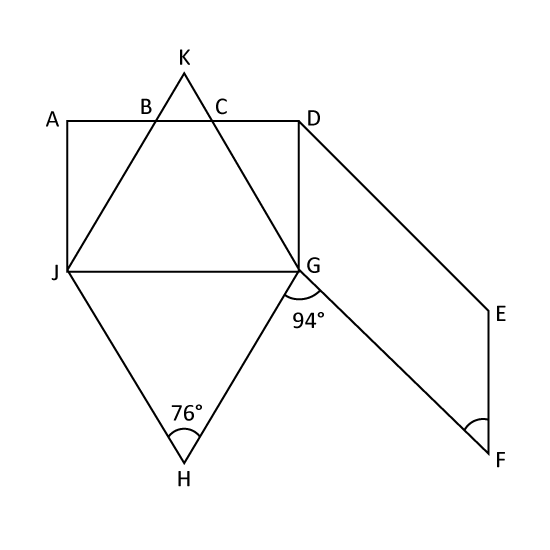
Level 3
In the figure, ADGJ is a rectangle, GHJK is a rhombus and DEFG is a parallelogram. ∠GHJ = 76° and ∠FGH = 94°.
- Find ∠CGD.
- Find ∠GFE.
Level 3
In the figure, ADGJ is a rectangle, GHJK is a rhombus and DEFG is a parallelogram. ∠GHJ = 76° and ∠FGH = 94°.
- Find ∠CGD.
- Find ∠GFE.
Image in this question is not available.
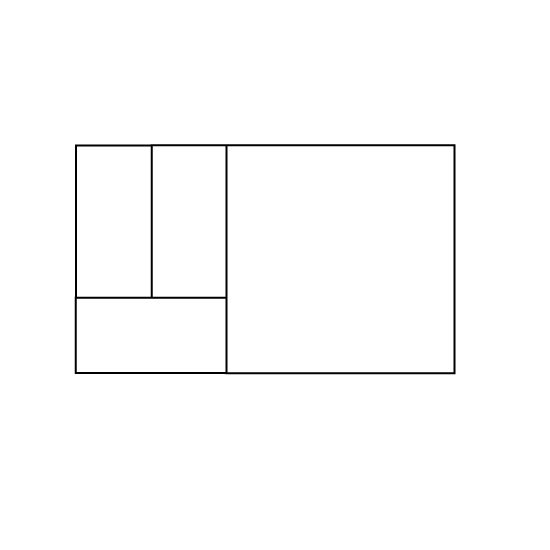
Level 3
Figure ABCD is made up of 3 identical rectangles and a square. The perimeter of the whole figure ABCD is 80 cm. What is the area of the figure ABCD?
Level 3
Figure ABCD is made up of 3 identical rectangles and a square. The perimeter of the whole figure ABCD is 80 cm. What is the area of the figure ABCD?
Image in this question is not available.
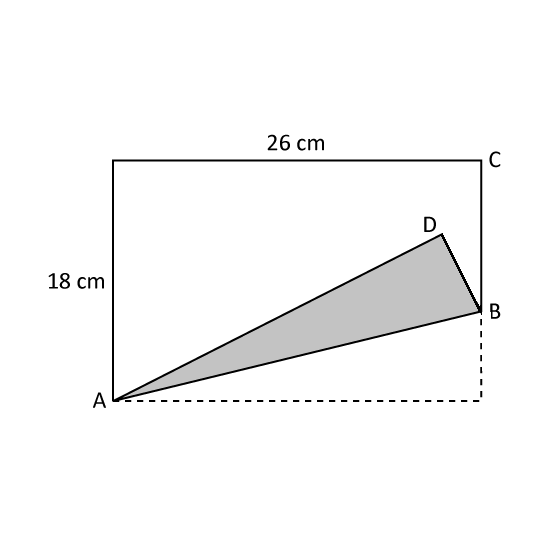
Level 3
In the figure, a rectangular piece of paper measuring 26 cm by 18 cm is folded at the Corner D in such a way that BD is 13 of its breadth. Find the area of Triangle ABD.
Level 3
In the figure, a rectangular piece of paper measuring 26 cm by 18 cm is folded at the Corner D in such a way that BD is 13 of its breadth. Find the area of Triangle ABD.
Image in this question is not available.
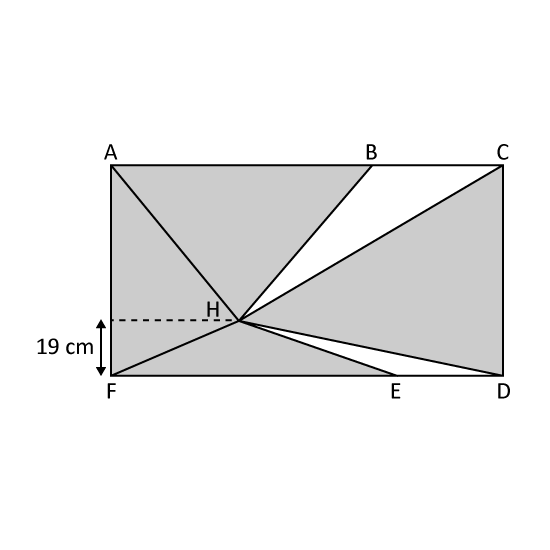
Level 3
Given that BC is longer than ED by 10 cm and CD = 42 cm. BC is 25 of AB and the total area of Triangle AHF and Triangle CHD is 1323 cm2. Find the area of the unshaded triangles.
Level 3
Given that BC is longer than ED by 10 cm and CD = 42 cm. BC is 25 of AB and the total area of Triangle AHF and Triangle CHD is 1323 cm2. Find the area of the unshaded triangles.
Image in this question is not available.
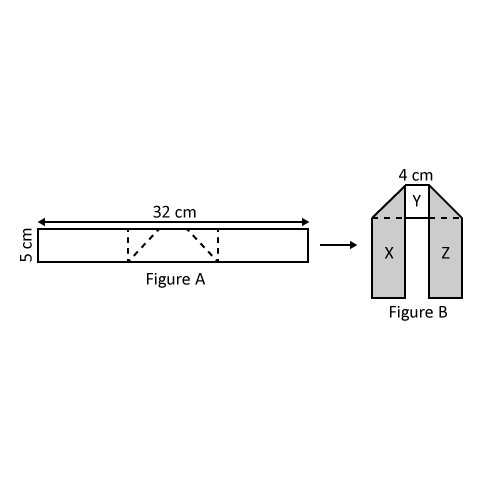
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Image in this question is not available.
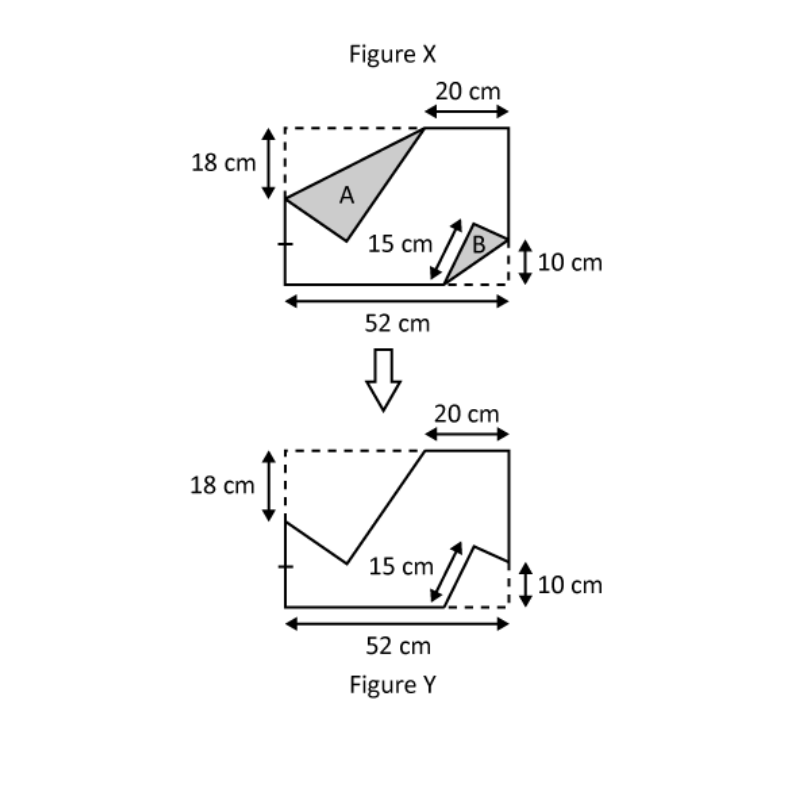
Level 3
Melvina folded a rectangular piece of paper, coloured on one side, to form Figure X as shown . She cut out the folded part A and B into the shape as shown in Figure Y. Find the area of Figure Y.
Level 3
Melvina folded a rectangular piece of paper, coloured on one side, to form Figure X as shown . She cut out the folded part A and B into the shape as shown in Figure Y. Find the area of Figure Y.
Image in this question is not available.
TRY FOR FREE
Level 3 PSLE
A plot of land which had an area of 876 m
2 was divided into three portions of equal width. These portions were fenced using 177 m of fence as shown.
- Find the length of AB.
- Find the perimeter of the plot of land.
Level 3 PSLE
A plot of land which had an area of 876 m
2 was divided into three portions of equal width. These portions were fenced using 177 m of fence as shown.
- Find the length of AB.
- Find the perimeter of the plot of land.
Image in this question is not available.
Level 3
Ben has a white rectangular card which is grey on the other side. He folds the card along its diagonal ED. Find
(a) ∠a
(b) ∠b
(c) ∠c
Level 3
Ben has a white rectangular card which is grey on the other side. He folds the card along its diagonal ED. Find
(a) ∠a
(b) ∠b
(c) ∠c
Image in this question is not available.