Level 3
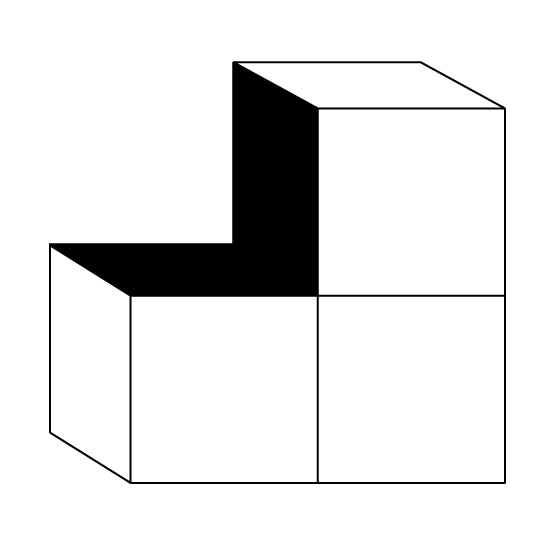
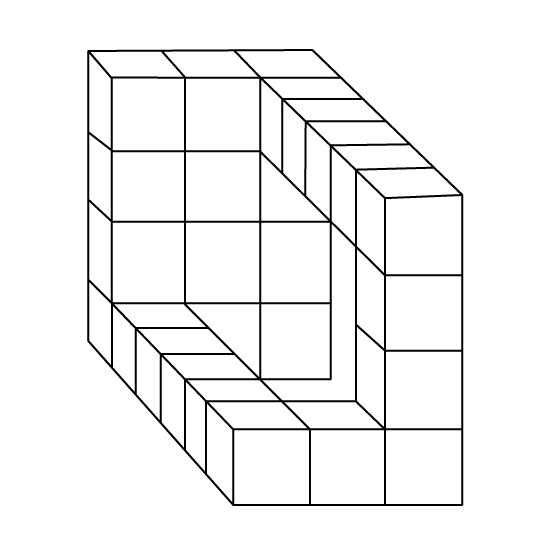
The figure is made up of identical cubes. The total area of the shaded faces is 338 cm2. Find the volume of the solid figure when we add 1 more of such cubes to it.
Level 3
The figure is made up of identical cubes. The total area of the shaded faces is 338 cm2. Find the volume of the solid figure when we add 1 more of such cubes to it.
Image in this question is not available.
Level 3
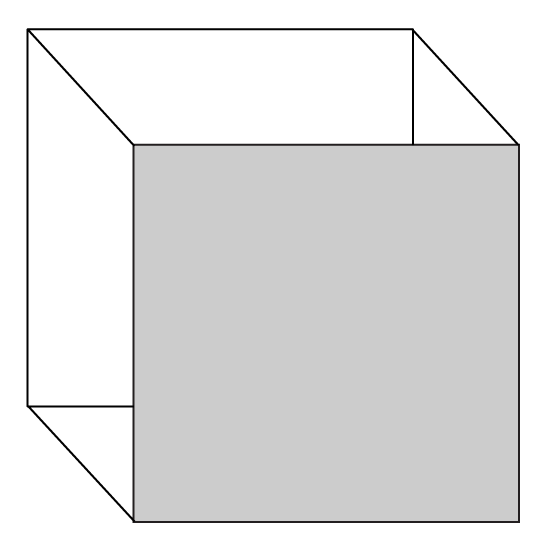
The figure shows a cube. The total length of all the edges of the cube is 156 cm.
- Find the area of the shaded face.
- Find the volume of the cube.
Level 3
The figure shows a cube. The total length of all the edges of the cube is 156 cm.
- Find the area of the shaded face.
- Find the volume of the cube.
Image in this question is not available.
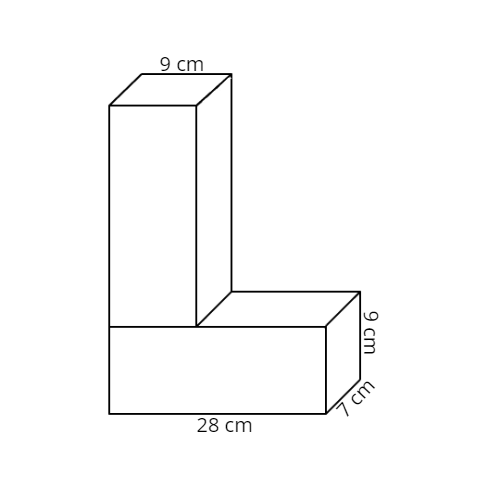
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Image in this question is not available.
Level 3 PSLE
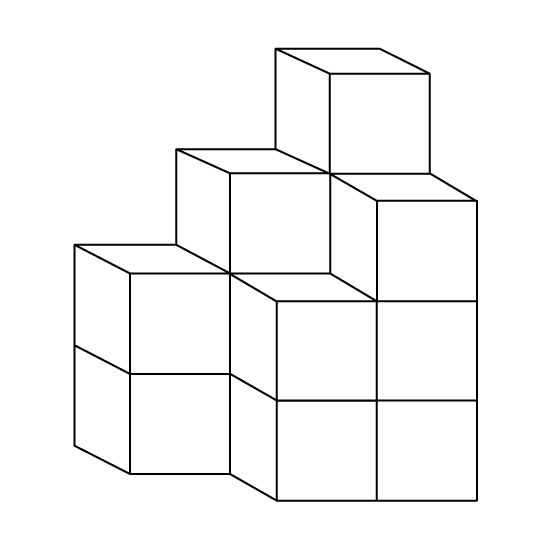
The figure shows a solid made up of identical cubes glued together. The surface area of the solid, including the base is painted blue. The volume of the solid is 1750 cm3. What is the total surface area that is painted blue?
Level 3 PSLE
The figure shows a solid made up of identical cubes glued together. The surface area of the solid, including the base is painted blue. The volume of the solid is 1750 cm3. What is the total surface area that is painted blue?
Image in this question is not available.
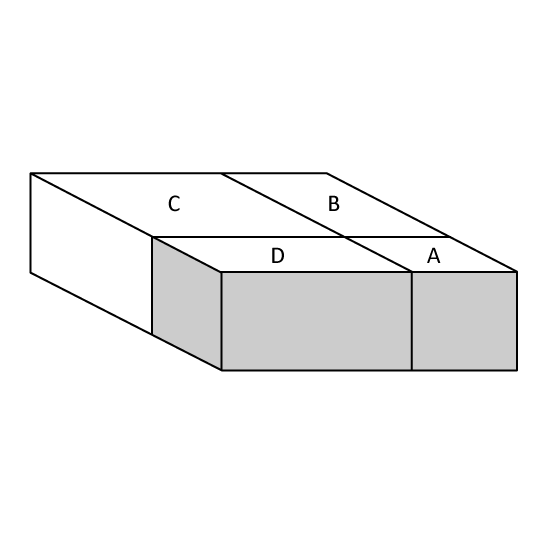
Level 3
This figure is not drawn to scale. A rectangular cuboid has been divided into 4 parts, A, B, C and D. The volume of A, B and C are in the ratio of 1 : 2 : 6. A is a cube and has a volume of 64 cm3. Find the total area of the shaded parts.
Level 3
This figure is not drawn to scale. A rectangular cuboid has been divided into 4 parts, A, B, C and D. The volume of A, B and C are in the ratio of 1 : 2 : 6. A is a cube and has a volume of 64 cm3. Find the total area of the shaded parts.
Image in this question is not available.
Level 3
Figure 1 shows a closed rectangular tank of dimensions 40 cm by 40 cm by 80 cm with a cube of edge 20 cm glued to its bottom left corner. The tank contains 70 litres of water. Figure 2 shows the same rectangular tank lying on its side. Find the height of the water level, in centimetres, corrected to 2 decimal places.
Level 3
Figure 1 shows a closed rectangular tank of dimensions 40 cm by 40 cm by 80 cm with a cube of edge 20 cm glued to its bottom left corner. The tank contains 70 litres of water. Figure 2 shows the same rectangular tank lying on its side. Find the height of the water level, in centimetres, corrected to 2 decimal places.
Image in this question is not available.
Level 3
The figure shows an empty transparent tank made from three containers. The two containers A and B on top are in the form of cuboids which have square bases of side 6 cm and 4 cm as shown in the figure. The bottom container is in the form of a cube of side 14 cm. 3.42ℓ of water are poured into the empty vase. Find the height of the water level from the base of the vase.
(1 litre = 1000 cm3)
Level 3
The figure shows an empty transparent tank made from three containers. The two containers A and B on top are in the form of cuboids which have square bases of side 6 cm and 4 cm as shown in the figure. The bottom container is in the form of a cube of side 14 cm. 3.42ℓ of water are poured into the empty vase. Find the height of the water level from the base of the vase.
(1 litre = 1000 cm3)
Image in this question is not available.
Level 3 PSLE
The figure shows an empty flower vase of height 40 cm. It is made from 2 containers. The top container is in the form of a cuboid which has a square base side 4 cm and height 28 cm. The bottom container is in the form of a cube of 12 cm. 2.16 litres of water is poured into the empty vase. What is the height of the water level from the base of the vase?
(1 litre = 1000 cm3 )
Level 3 PSLE
The figure shows an empty flower vase of height 40 cm. It is made from 2 containers. The top container is in the form of a cuboid which has a square base side 4 cm and height 28 cm. The bottom container is in the form of a cube of 12 cm. 2.16 litres of water is poured into the empty vase. What is the height of the water level from the base of the vase?
(1 litre = 1000 cm3 )
Image in this question is not available.
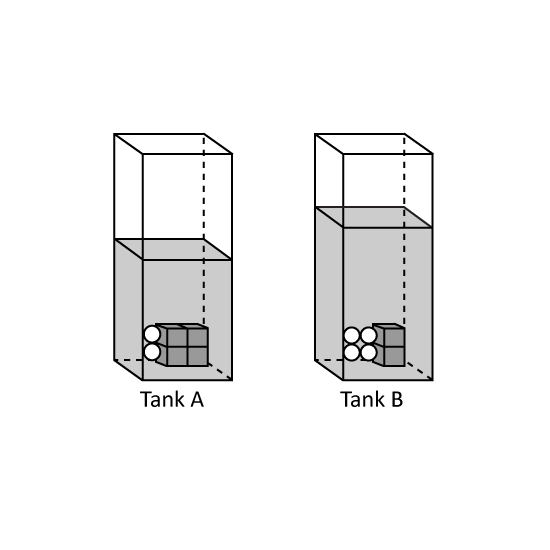
Level 3
The figure shows 2 identical containers each holding 202 cm3 of water. The volumes of the water, the cubes and balls in Tank G and Tank H are 646 cm3 and 1183 cm3 respectively. What is the volume of each ball? Give the answer in cm3.
Level 3
The figure shows 2 identical containers each holding 202 cm3 of water. The volumes of the water, the cubes and balls in Tank G and Tank H are 646 cm3 and 1183 cm3 respectively. What is the volume of each ball? Give the answer in cm3.
Image in this question is not available.
Level 3
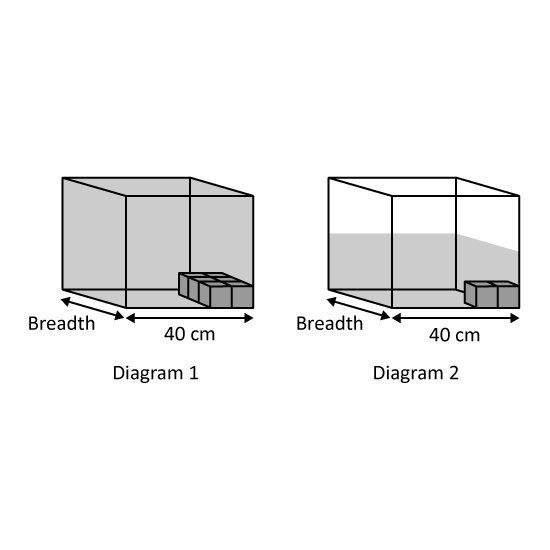
The diagrams are not drawn to scale. Diagram 1 shows a rectangular tank containing 6 identical cubes and filled to the brim. It had a length of 40 cm and a breadth of 10 cm. In Diagram 2, four cubes were removed from the same tank and the water level dropped by 2.16 cm.
After that, a certain amount of water was drained off the tank until the water level reaches the same height as the remaining cubes. Find the volume of the water in the tank in Diagram 2 in the end. Give the answer in litres.
Level 3
The diagrams are not drawn to scale. Diagram 1 shows a rectangular tank containing 6 identical cubes and filled to the brim. It had a length of 40 cm and a breadth of 10 cm. In Diagram 2, four cubes were removed from the same tank and the water level dropped by 2.16 cm.
After that, a certain amount of water was drained off the tank until the water level reaches the same height as the remaining cubes. Find the volume of the water in the tank in Diagram 2 in the end. Give the answer in litres.
Image in this question is not available.
Level 3
34 of a rectangular tank, 90 cm by 8 cm by 5 cm, is filled with water. A cubical container of edge 18 cm is filled with water to a depth of 15 cm. If the water in the rectangular tank is transferred to the cubical container until it is filled to its brim, how many litres of water will be left in the rectangular tank?
3 m
Image in this question is not available.
Level 3
A rectangular tank measuring 35 cm by 26 cm by 12 cm is completely filled with oil. Oil from the tank is poured into an empty cubical container of edge 18 cm until the cubical container is half-filled. What is the height of the oil in the tank after some oil is poured out? Correct the answer to 1 decimal place.
3 m
Image in this question is not available.
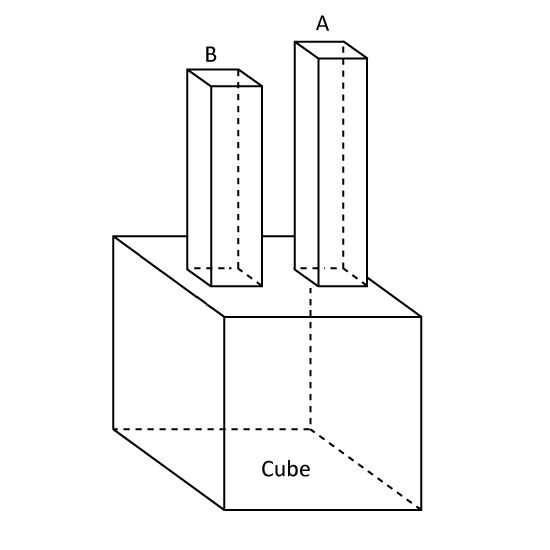
Level 3
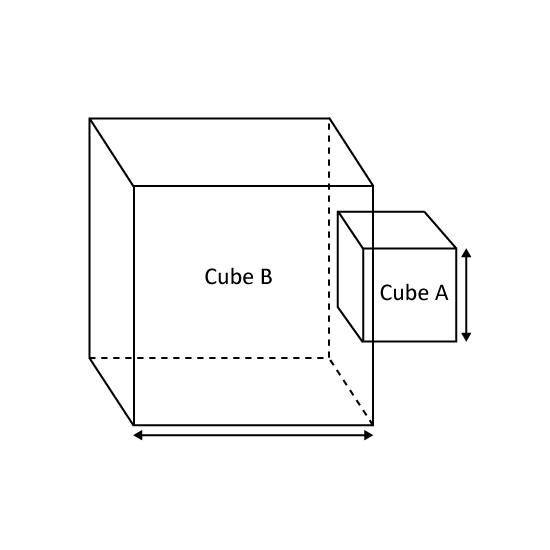
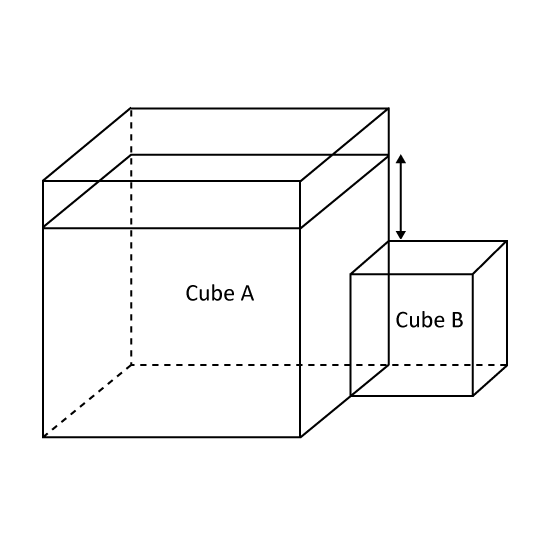
The figure shows an empty container. It is made from two cubical tanks. Tanks, Cube A and Cube B, are of sides 10 cm and 20 cm respectively. Cube A is attached to the centre of one of the sides of the Cube B. 5 litres of water is poured into the container such that water flows in to fill part of Cube A. What is the height of the water level in the container? Round off the answer to one decimal place.
Level 3
The figure shows an empty container. It is made from two cubical tanks. Tanks, Cube A and Cube B, are of sides 10 cm and 20 cm respectively. Cube A is attached to the centre of one of the sides of the Cube B. 5 litres of water is poured into the container such that water flows in to fill part of Cube A. What is the height of the water level in the container? Round off the answer to one decimal place.
Image in this question is not available.
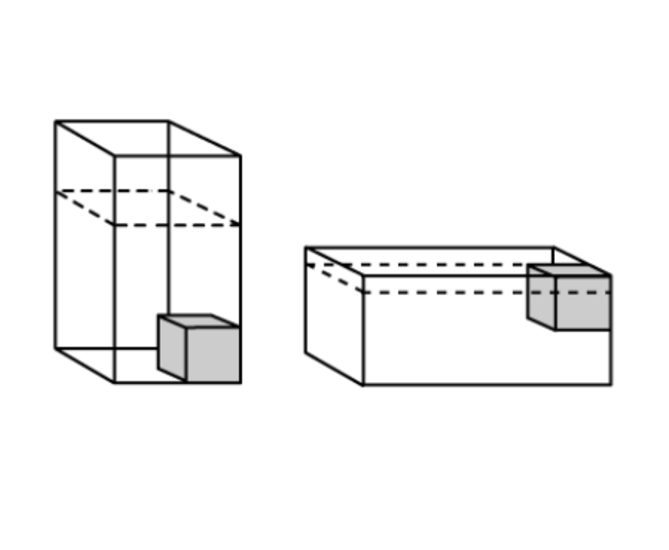
Level 3 PSLE
Ann had some identitical cuboids with square base and height, h. She then stacked the cuboid to form the 2 towers. The figure shows the front view and the side views of the 2 towers.
- Find h.
- Find the volume of the cuboid.
Level 3 PSLE
Ann had some identitical cuboids with square base and height, h. She then stacked the cuboid to form the 2 towers. The figure shows the front view and the side views of the 2 towers.
- Find h.
- Find the volume of the cuboid.
Image in this question is not available.
Level 3
A rectangular block is sprayed grey on all the six faces before it is cut into 36 identical cubes as shown in the diagram. The total surface area of the 36 individual cubes is 576 cm2 more than the surface area of the original block that is sprayed grey. What is the volume of the rectangular block?
Level 3
A rectangular block is sprayed grey on all the six faces before it is cut into 36 identical cubes as shown in the diagram. The total surface area of the 36 individual cubes is 576 cm2 more than the surface area of the original block that is sprayed grey. What is the volume of the rectangular block?
Image in this question is not available.
Level 3
The figure shows a rectangular glass tank partly filled with
1-cm cubes. After adding 1 extra cube,
- How many more cubes are needed to Tank completely?
- What is the volume of glass tank?
Level 3
The figure shows a rectangular glass tank partly filled with
1-cm cubes. After adding 1 extra cube,
- How many more cubes are needed to Tank completely?
- What is the volume of glass tank?
Image in this question is not available.
Level 3
The figure is made up of identical cubes. If the volume of the solid is 702 cm
3,
- Find the total surface area of the figure.
- How many more of such cubes is to be added to form a cube of side 54 cm?
Level 3
The figure is made up of identical cubes. If the volume of the solid is 702 cm
3,
- Find the total surface area of the figure.
- How many more of such cubes is to be added to form a cube of side 54 cm?
Image in this question is not available.
Level 3
The figure is not drawn to scale. It shows a tank made from two connected cubical containers, Cube A and Cube B. The tank is filled with some water. Cube A is 34 filled with 6000 mℓ of water while Cube B is completely filled with water. The height of the water level in Cube A is 4 cm higher than that in Cube B. Water is then drained from the tank and the height of the new water level is 5 cm. What is the volume of the water drained in mℓ?
Level 3
The figure is not drawn to scale. It shows a tank made from two connected cubical containers, Cube A and Cube B. The tank is filled with some water. Cube A is 34 filled with 6000 mℓ of water while Cube B is completely filled with water. The height of the water level in Cube A is 4 cm higher than that in Cube B. Water is then drained from the tank and the height of the new water level is 5 cm. What is the volume of the water drained in mℓ?
Image in this question is not available.
Level 3 PSLE
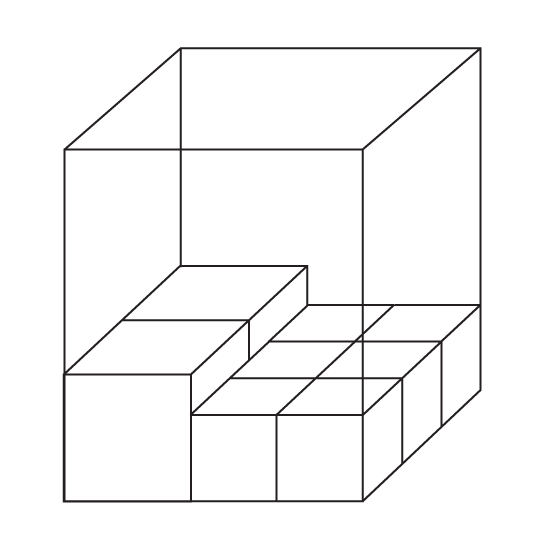
David has 8 large cubes and some small cubes. He placed them in a rectangular tank. The tank was filled to the brim exactly. The diagram shows the first layer of cubes.
- How many small cubes does David have?
- The volume of the tank is 504 cm3. If the large cubes took up 37 of the tank, What is the length of the edge of one small cube?
Level 3 PSLE
David has 8 large cubes and some small cubes. He placed them in a rectangular tank. The tank was filled to the brim exactly. The diagram shows the first layer of cubes.
- How many small cubes does David have?
- The volume of the tank is 504 cm3. If the large cubes took up 37 of the tank, What is the length of the edge of one small cube?
Image in this question is not available.
Level 3 PSLE
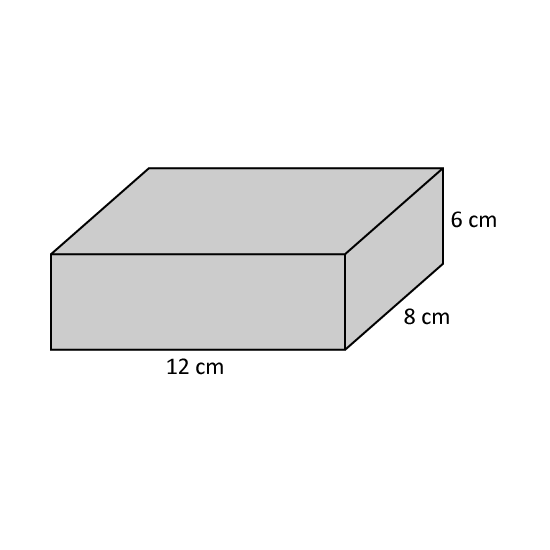
Ray had a rectangular block of wood 12 cm by 8 cm by 6 cm. He painted all the faces of the block.
- What is the total painted area?
- Ray then cut the block into 1-cm cubes. How many of these cubes have none of the faces painted?
- How many of these cubes have 2 of the faces painted?
Level 3 PSLE
Ray had a rectangular block of wood 12 cm by 8 cm by 6 cm. He painted all the faces of the block.
- What is the total painted area?
- Ray then cut the block into 1-cm cubes. How many of these cubes have none of the faces painted?
- How many of these cubes have 2 of the faces painted?
Image in this question is not available.