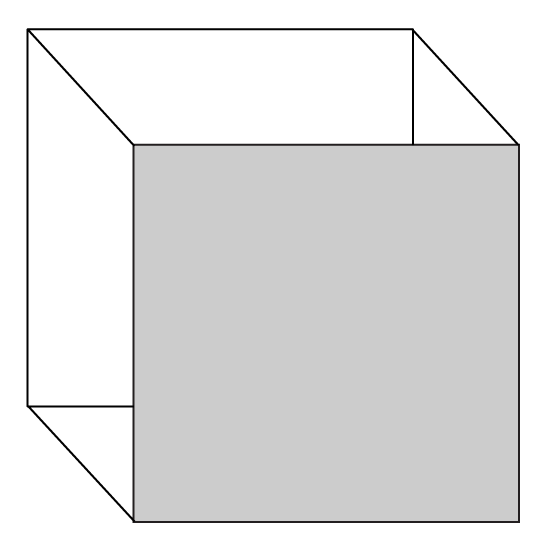
Level 2
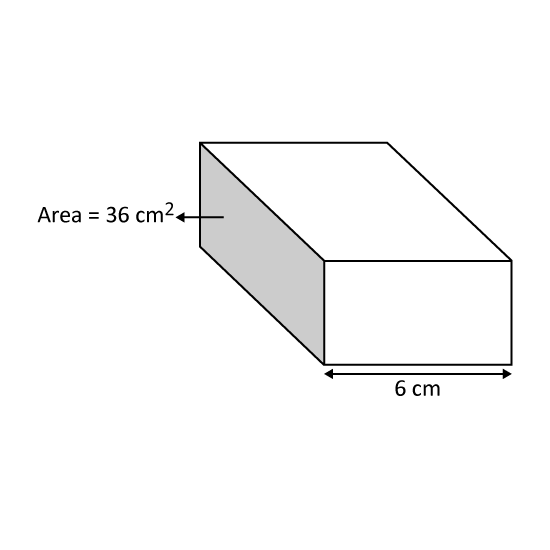
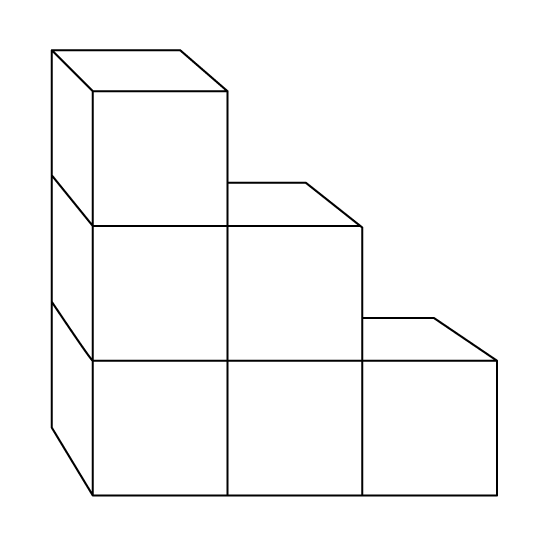
The shaded surface area of the rectangular box shown is 36 cm2. What is the volume of the box?
Level 2
The shaded surface area of the rectangular box shown is 36 cm2. What is the volume of the box?
Image in this question is not available.
Level 2
The total area of the six faces of a cubical box is 96 cm2. What is the volume of the cubical box?
2 m
Image in this question is not available.
Level 1
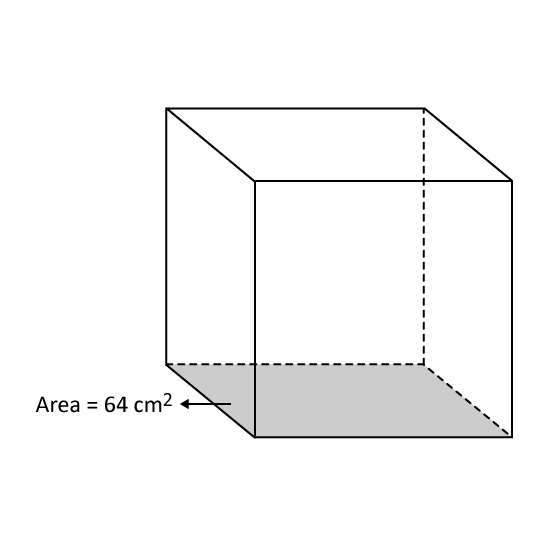
The base area of the cubical box is 64 cm2. What is the volume of the box?
Level 1
The base area of the cubical box is 64 cm2. What is the volume of the box?
Image in this question is not available.
Level 3
The total surface area of a cube is 6 m2. What is the volume of the cube?
3 m
Image in this question is not available.
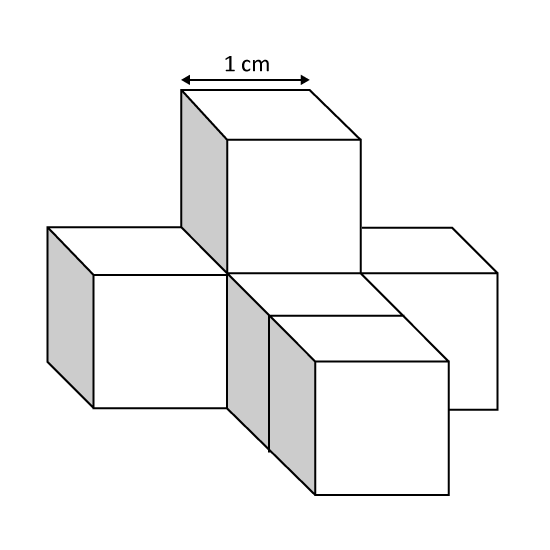
Level 3
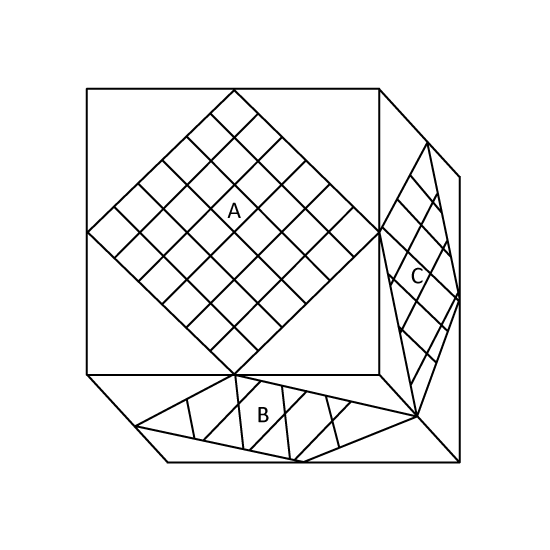
The figure shows a cube with 3 painted parts A, B and C. These painted parts are of the same area and they are touching the midpoints of the sides of the cube. The total area of the painted parts is 96 cm2. Find the volume of 3 such cubes.
Level 3
The figure shows a cube with 3 painted parts A, B and C. These painted parts are of the same area and they are touching the midpoints of the sides of the cube. The total area of the painted parts is 96 cm2. Find the volume of 3 such cubes.
Image in this question is not available.
Level 3
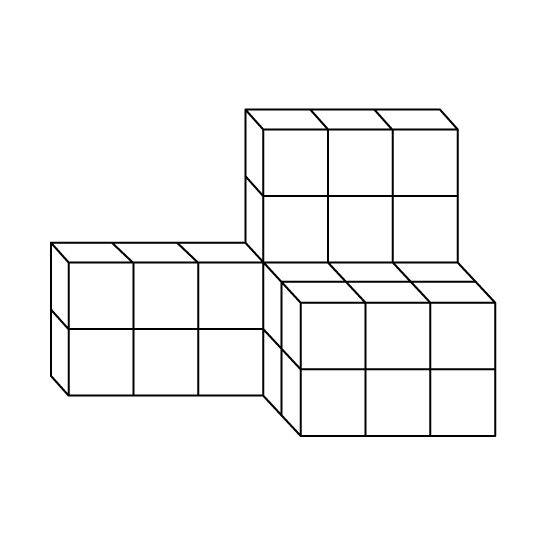
The figure is made up of identical cubes. The total area of the shaded faces is 338 cm2. Find the volume of the solid figure when we add 1 more of such cubes to it.
Level 3
The figure is made up of identical cubes. The total area of the shaded faces is 338 cm2. Find the volume of the solid figure when we add 1 more of such cubes to it.
Image in this question is not available.
Level 3
The figure shows a cube. The total length of all the edges of the cube is 156 cm.
- Find the area of the shaded face.
- Find the volume of the cube.
Level 3
The figure shows a cube. The total length of all the edges of the cube is 156 cm.
- Find the area of the shaded face.
- Find the volume of the cube.
Image in this question is not available.
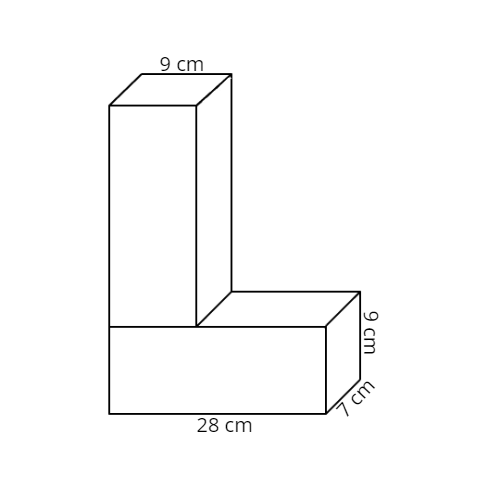
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Image in this question is not available.
Level 3 PSLE
The figure shows a solid made up of identical cubes glued together. The surface area of the solid, including the base is painted blue. The volume of the solid is 1750 cm3. What is the total surface area that is painted blue?
Level 3 PSLE
The figure shows a solid made up of identical cubes glued together. The surface area of the solid, including the base is painted blue. The volume of the solid is 1750 cm3. What is the total surface area that is painted blue?
Image in this question is not available.
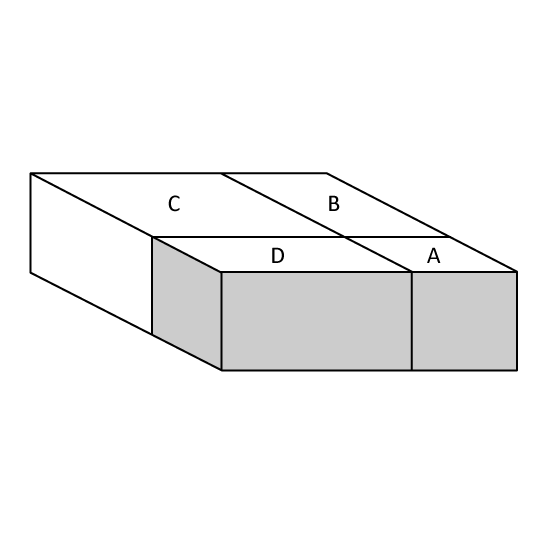
Level 3
This figure is not drawn to scale. A rectangular cuboid has been divided into 4 parts, A, B, C and D. The volume of A, B and C are in the ratio of 1 : 2 : 6. A is a cube and has a volume of 64 cm3. Find the total area of the shaded parts.
Level 3
This figure is not drawn to scale. A rectangular cuboid has been divided into 4 parts, A, B, C and D. The volume of A, B and C are in the ratio of 1 : 2 : 6. A is a cube and has a volume of 64 cm3. Find the total area of the shaded parts.
Image in this question is not available.
Level 3
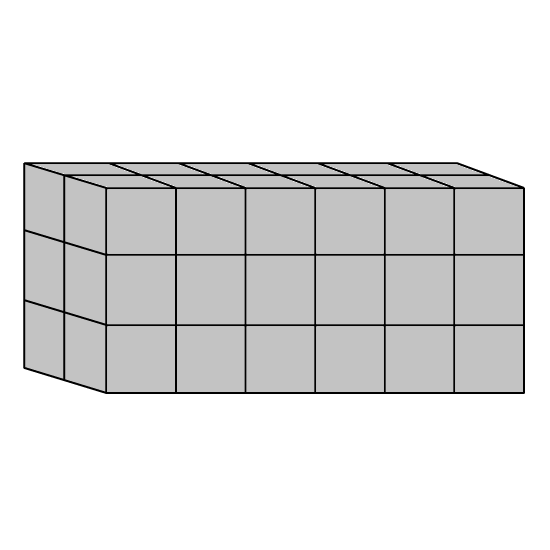
The solid figure is made up of 6 identical cubes of edge 7 cm.
- Find the volume of the solid figure.
- Find the total surface area of the solid figure.
Level 3
The solid figure is made up of 6 identical cubes of edge 7 cm.
- Find the volume of the solid figure.
- Find the total surface area of the solid figure.
Image in this question is not available.
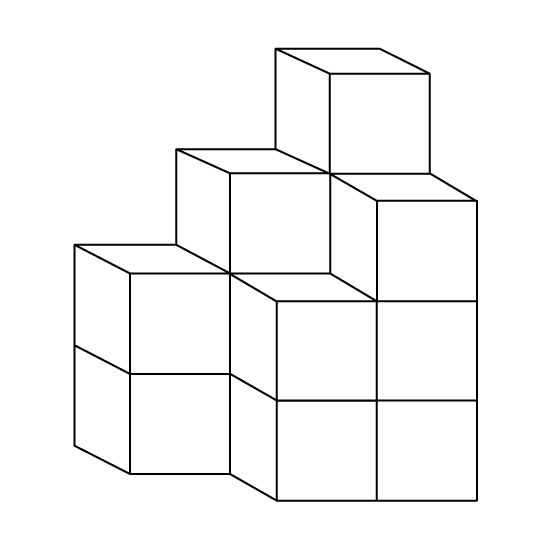
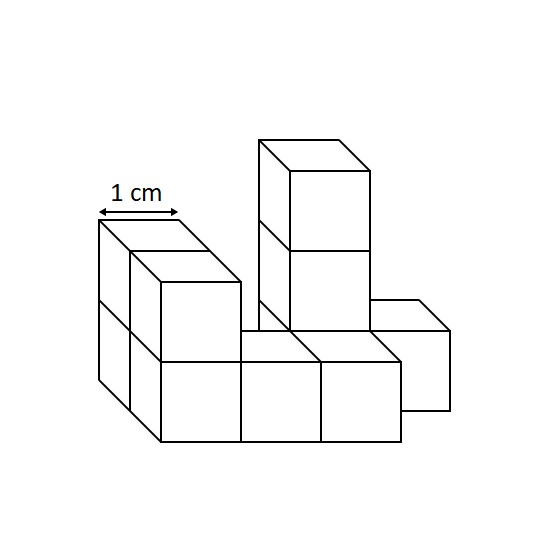
Level 2
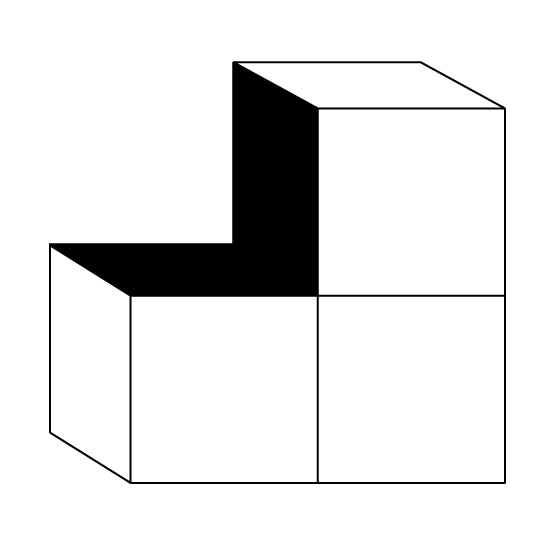
The figure is made of unit cubes. If Joan were to dip the figure in red paint, what area of the figure would be painted?
Level 2
The figure is made of unit cubes. If Joan were to dip the figure in red paint, what area of the figure would be painted?
Image in this question is not available.
Level 2
The figure is made of unit cubes. If Joan were to dip the figure in red paint, what area of the figure would be painted?
Level 2
The figure is made of unit cubes. If Joan were to dip the figure in red paint, what area of the figure would be painted?
Image in this question is not available.
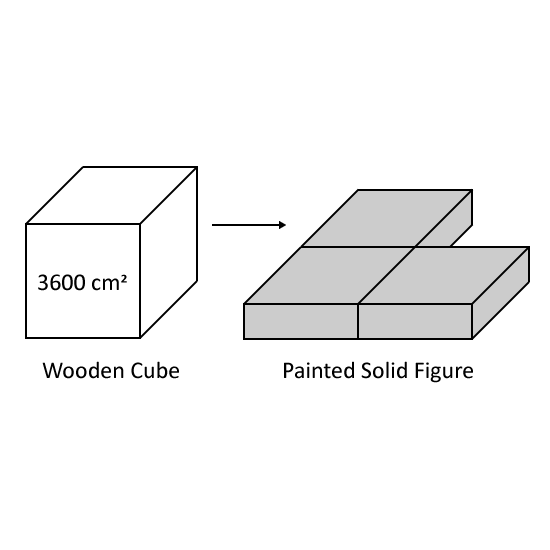
Level 3
The area of one face of the wooden cube is 3600 cm2. A carpenter cut the wooden cube into three cuboids of identical size. After gluing the cuboids together to make a solid figure as shown, he painted all the surfaces of the solid figure red. What was the total surface area of the solid figure that had been painted red?
Level 3
The area of one face of the wooden cube is 3600 cm2. A carpenter cut the wooden cube into three cuboids of identical size. After gluing the cuboids together to make a solid figure as shown, he painted all the surfaces of the solid figure red. What was the total surface area of the solid figure that had been painted red?
Image in this question is not available.
Level 3
The solid figure is made up of 3-cm cubes.
- Find its volume.
- If the solid figure is placed on the floor and some paint is poured onto the solid figure such that all the exposed sides are coated with paint, how many cubes will have only two of its faces covered with paint?
Level 3
The solid figure is made up of 3-cm cubes.
- Find its volume.
- If the solid figure is placed on the floor and some paint is poured onto the solid figure such that all the exposed sides are coated with paint, how many cubes will have only two of its faces covered with paint?
Image in this question is not available.
Level 2
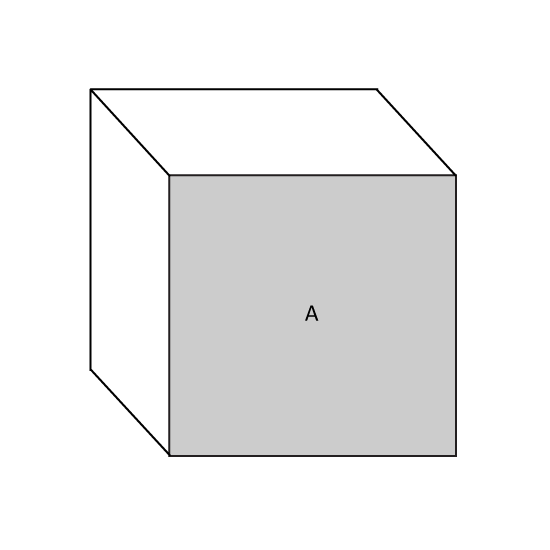
The figure shown on the right is a cube. The perimeter of Face A is 16 cm. What is the total area of all the faces of the cube?
Level 2
The figure shown on the right is a cube. The perimeter of Face A is 16 cm. What is the total area of all the faces of the cube?
Image in this question is not available.
Level 3
A rectangular block is sprayed grey on all the six faces before it is cut into 36 identical cubes as shown in the diagram. The total surface area of the 36 individual cubes is 576 cm2 more than the surface area of the original block that is sprayed grey. What is the volume of the rectangular block?
Level 3
A rectangular block is sprayed grey on all the six faces before it is cut into 36 identical cubes as shown in the diagram. The total surface area of the 36 individual cubes is 576 cm2 more than the surface area of the original block that is sprayed grey. What is the volume of the rectangular block?
Image in this question is not available.
Level 3
The figure is made up of identical cubes. If the volume of the solid is 702 cm
3,
- Find the total surface area of the figure.
- How many more of such cubes is to be added to form a cube of side 54 cm?
Level 3
The figure is made up of identical cubes. If the volume of the solid is 702 cm
3,
- Find the total surface area of the figure.
- How many more of such cubes is to be added to form a cube of side 54 cm?
Image in this question is not available.
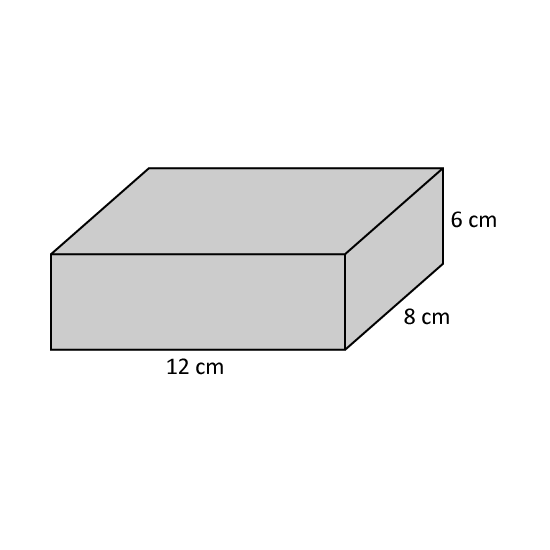
Level 3 PSLE
Ray had a rectangular block of wood 12 cm by 8 cm by 6 cm. He painted all the faces of the block.
- What is the total painted area?
- Ray then cut the block into 1-cm cubes. How many of these cubes have none of the faces painted?
- How many of these cubes have 2 of the faces painted?
Level 3 PSLE
Ray had a rectangular block of wood 12 cm by 8 cm by 6 cm. He painted all the faces of the block.
- What is the total painted area?
- Ray then cut the block into 1-cm cubes. How many of these cubes have none of the faces painted?
- How many of these cubes have 2 of the faces painted?
Image in this question is not available.
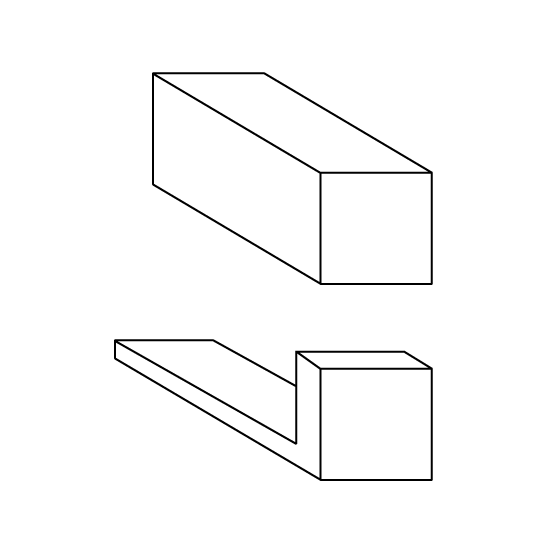
Level 3
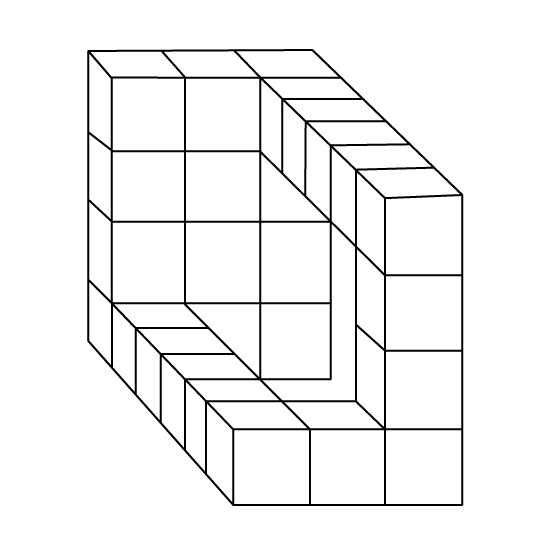
The figure shows a wooden cuboid that measures 125 cm by 20 cm by 20 cm.
- Find the maximum number of 3-cm cubes that can be cut from the wooden cuboid.
- Find the total surface area of the L-shaped block after cutting.
Level 3
The figure shows a wooden cuboid that measures 125 cm by 20 cm by 20 cm.
- Find the maximum number of 3-cm cubes that can be cut from the wooden cuboid.
- Find the total surface area of the L-shaped block after cutting.
Image in this question is not available.