Level 3
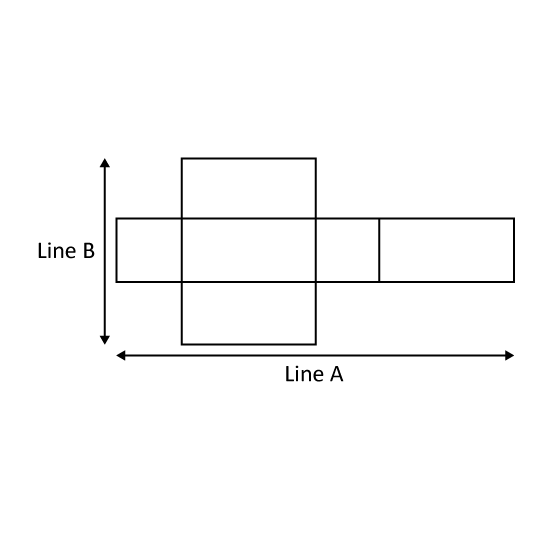
The figure is not drawn to scale. It shows the net of a solid. It is made up of 4 identical rectangles and 2 identical squares. Line A is 30 cm long and Line B is 15 cm long.
- Find the volume of the solid.
- This solid is a cardboard carton containing small boxes of sweets. Each box of sweets is 3 cm by 2 cm by 1 cm. If all these small boxes of sweets in the carton occupy more than 75% of the carton's volume, what is the minimum number of small boxes of sweets in the carton?
Level 3
The figure is not drawn to scale. It shows the net of a solid. It is made up of 4 identical rectangles and 2 identical squares. Line A is 30 cm long and Line B is 15 cm long.
- Find the volume of the solid.
- This solid is a cardboard carton containing small boxes of sweets. Each box of sweets is 3 cm by 2 cm by 1 cm. If all these small boxes of sweets in the carton occupy more than 75% of the carton's volume, what is the minimum number of small boxes of sweets in the carton?
Image in this question is not available.
Level 3
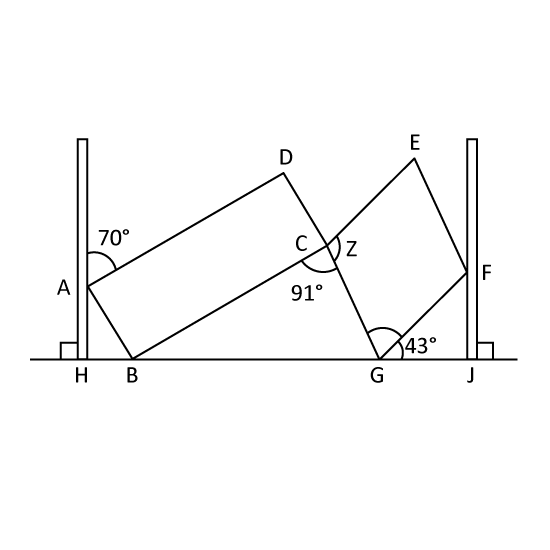
In the figure, not drawn to scale, shows a rhombus and a rectangle lined up between two poles. Find ∠z.
Level 3
In the figure, not drawn to scale, shows a rhombus and a rectangle lined up between two poles. Find ∠z.
Image in this question is not available.
Level 3
The perimeter of the rectangular base of a tank is 400 cm. The ratio of its length to its breadth is 3 : 2. When 48 ℓ of water are poured into the tank, 25 of it is filled. Find the height of the tank.
4 m
Image in this question is not available.
Level 3 PSLE
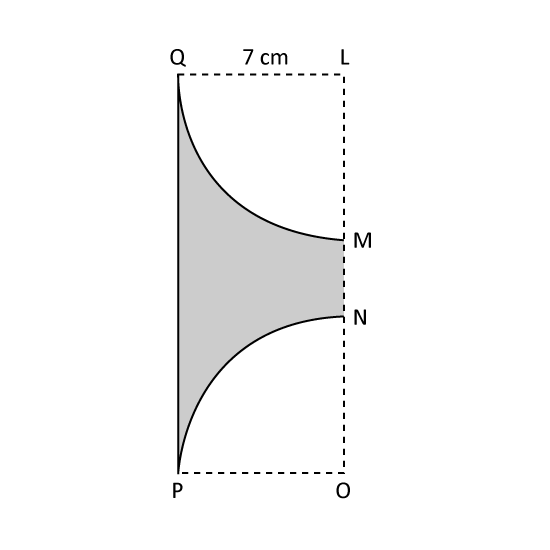
LOPQ is a rectangular cardboard with LQ = 7 cm. Two quarter circles have been cut from it as shown. The remaining cardboard, which is the shaded part, has an area of 56 cm2. Using π = 227, find the length of MN.
Level 3 PSLE
LOPQ is a rectangular cardboard with LQ = 7 cm. Two quarter circles have been cut from it as shown. The remaining cardboard, which is the shaded part, has an area of 56 cm2. Using π = 227, find the length of MN.
Image in this question is not available.
Level 3
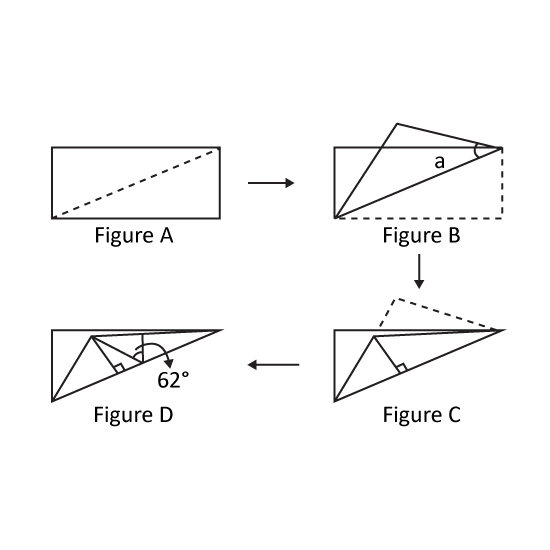
A rectangular piece of paper is folded along the diagonal as shown in Figure B. It is folded again as shown in Figure C before the last fold in Figure D. If the angle is 62° in Figure D, what is ∠a?
Level 3
A rectangular piece of paper is folded along the diagonal as shown in Figure B. It is folded again as shown in Figure C before the last fold in Figure D. If the angle is 62° in Figure D, what is ∠a?
Image in this question is not available.
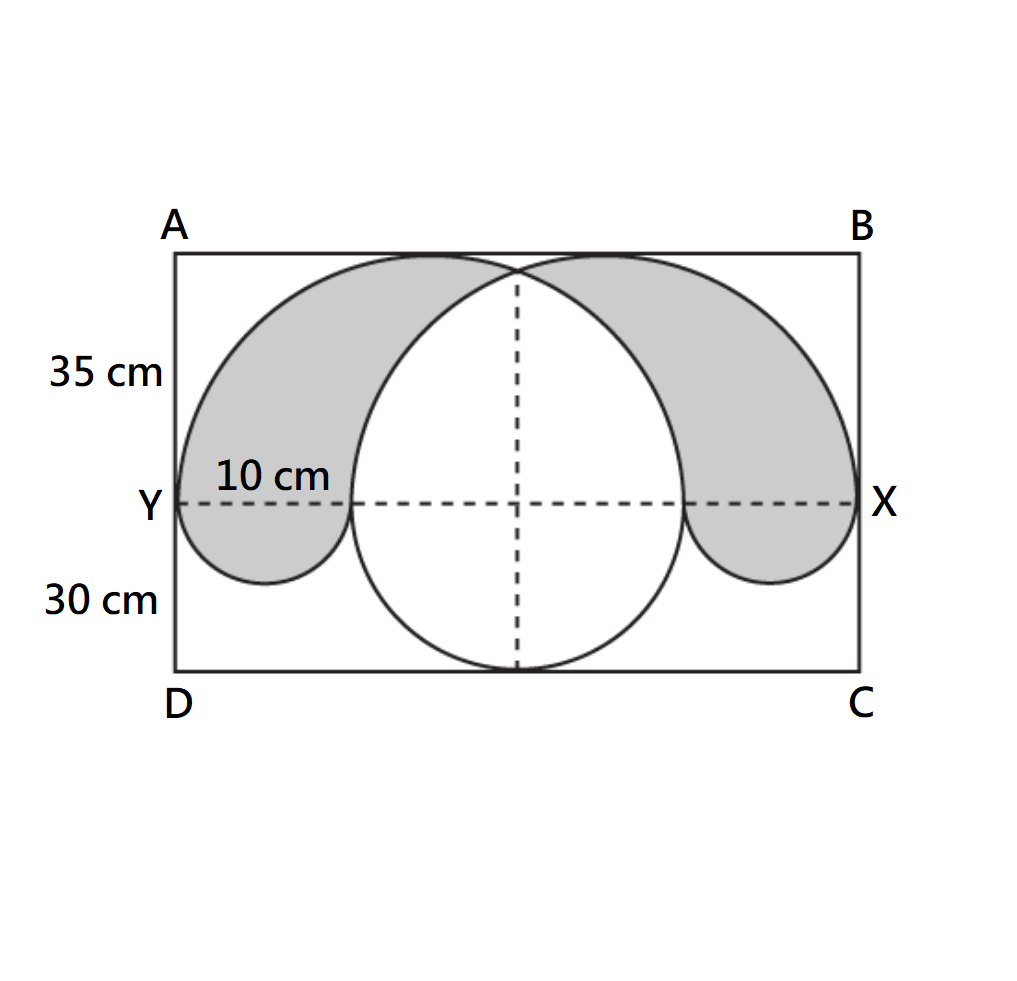
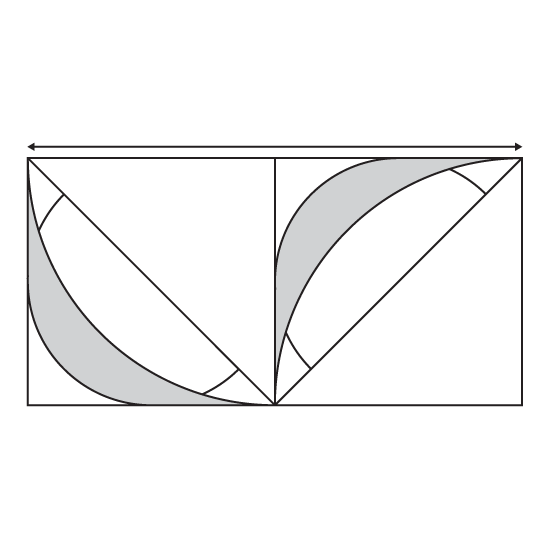
Level 3
The figure, not drawn to scale, is made up of semicircles in a rectangle ABCD. XY is the
common baseline for all the semi-circles.
- Find the length of AB.
- Using the calculator π, find the perimeter of the shaded parts. Give the answer correct to 2 decimal places.
Level 3
The figure, not drawn to scale, is made up of semicircles in a rectangle ABCD. XY is the
common baseline for all the semi-circles.
- Find the length of AB.
- Using the calculator π, find the perimeter of the shaded parts. Give the answer correct to 2 decimal places.
Image in this question is not available.
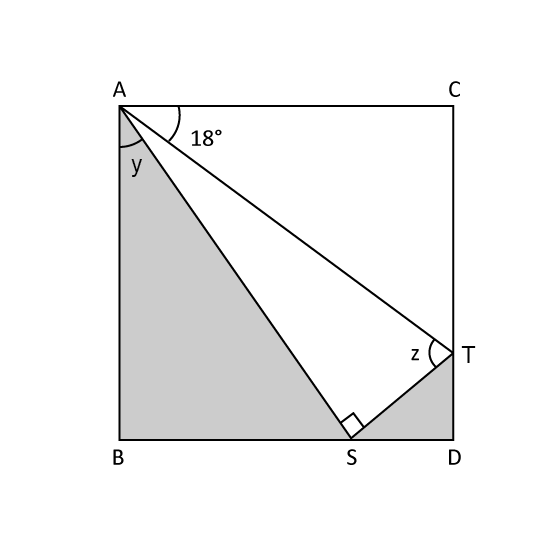
Level 3
The figure shows a rectangle ABCD being folded along AT. Given that ∠TAC = 18° find
- ∠y
- ∠z
Level 3
The figure shows a rectangle ABCD being folded along AT. Given that ∠TAC = 18° find
- ∠y
- ∠z
Image in this question is not available.
Level 3
The figure is not drawn to scale. EFCH is a square. ABCD and CXYZ are similar rectangles which overlap to form ∠s. Given that ∠FCX = 37° and that ∠HCD = ∠BCH, find ∠s.
Level 3
The figure is not drawn to scale. EFCH is a square. ABCD and CXYZ are similar rectangles which overlap to form ∠s. Given that ∠FCX = 37° and that ∠HCD = ∠BCH, find ∠s.
Image in this question is not available.
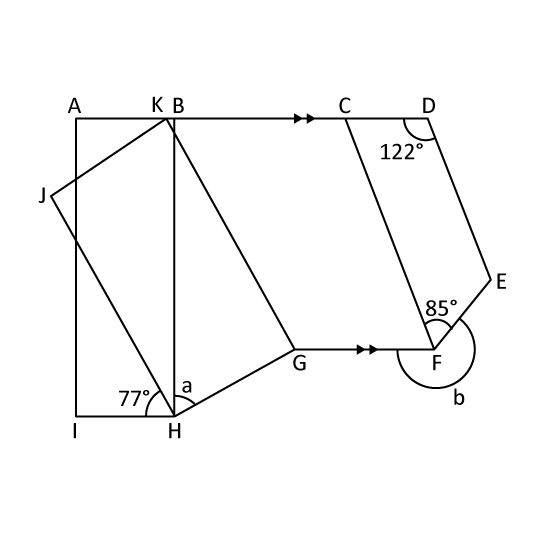
Level 3
In the figure, not drawn to scale, two rectangles, ABHI and GHJK overlap each other as shown. Given that AD // GF and CF // DE.
- Find ∠a.
- Find ∠b.
Level 3
In the figure, not drawn to scale, two rectangles, ABHI and GHJK overlap each other as shown. Given that AD // GF and CF // DE.
- Find ∠a.
- Find ∠b.
Image in this question is not available.
Level 3
A rectangular piece of paper is folded along the dotted line as shown. Find
- ∠a
- ∠b.
Level 3
A rectangular piece of paper is folded along the dotted line as shown. Find
- ∠a
- ∠b.
Image in this question is not available.
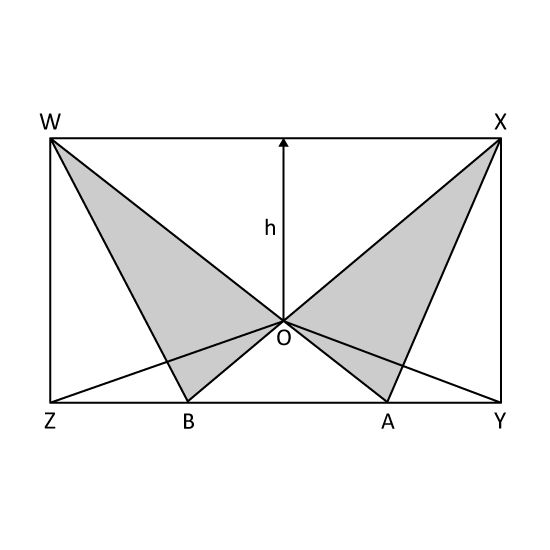
Level 3
In the figure, WXYZ is a rectangle. h = 20 cm, WX = 30 cm, XY = 24 cm. Find the area of the shaded parts.
Level 3
In the figure, WXYZ is a rectangle. h = 20 cm, WX = 30 cm, XY = 24 cm. Find the area of the shaded parts.
Image in this question is not available.
Level 3
The figure shows 2 quarter circles and a rectangle. The radius of the big quarter circle is 10 cm. The radius of the small quarter circle is 5 cm. Find the difference in area between the two shaded parts P and Q. (Take π = 3.14 and give the answer correct to 1 decimal place)
Answer: 5.7 cm2
Level 3
The figure shows 2 quarter circles and a rectangle. The radius of the big quarter circle is 10 cm. The radius of the small quarter circle is 5 cm. Find the difference in area between the two shaded parts P and Q. (Take π = 3.14 and give the answer correct to 1 decimal place)
Answer: 5.7 cm2
Image in this question is not available.
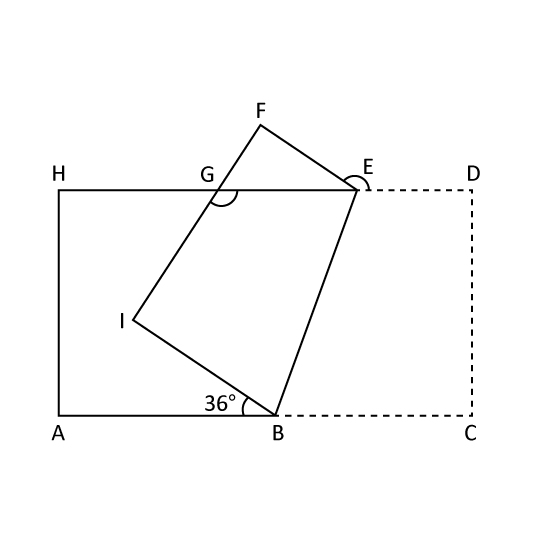
Level 3
A rectangular piece of paper was folded as shown. Find ∠EGI.
Level 3
A rectangular piece of paper was folded as shown. Find ∠EGI.
Image in this question is not available.
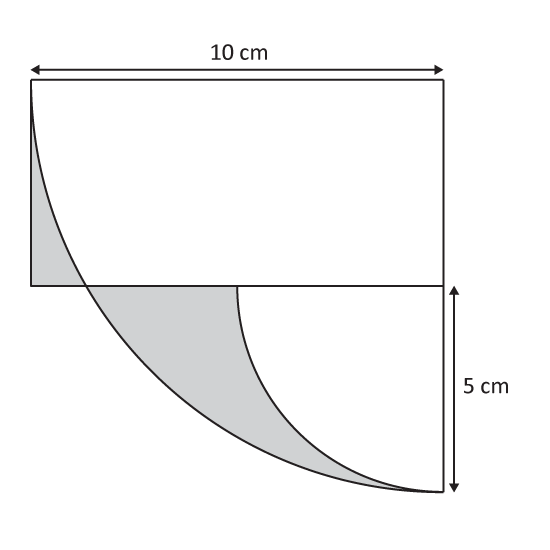
Level 3
The figure shows a rectangle with 2 identical semicircles and quadrants within It. The length of the rectangle is 10 cm. Find the area of the shaded part. (Take π = 3.14)
Level 3
The figure shows a rectangle with 2 identical semicircles and quadrants within It. The length of the rectangle is 10 cm. Find the area of the shaded part. (Take π = 3.14)
Image in this question is not available.
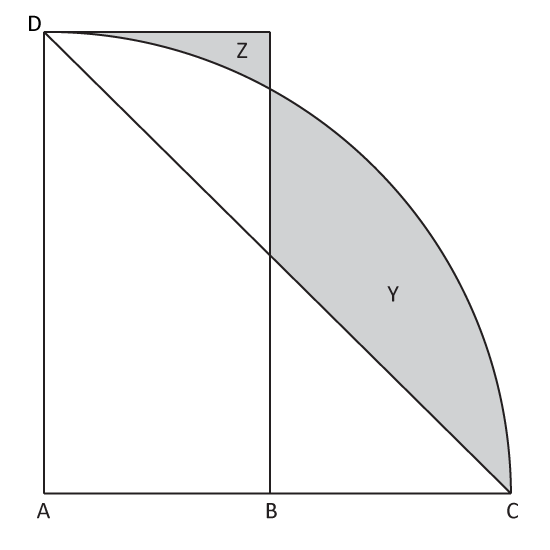
Level 3
The figure consists of a rectangle, a quadrant and an isosceles triangle. Given that the radius of the quadrant is 10 cm and B is the midpoint of Line AC, find the difference between the shaded areas Y and Z. Express the answer in nearest whole number.
(Take π = 3.14)
Level 3
The figure consists of a rectangle, a quadrant and an isosceles triangle. Given that the radius of the quadrant is 10 cm and B is the midpoint of Line AC, find the difference between the shaded areas Y and Z. Express the answer in nearest whole number.
(Take π = 3.14)
Image in this question is not available.
Level 3
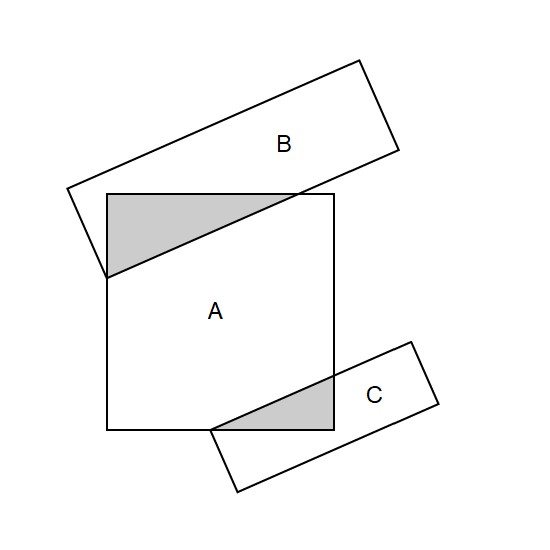
The figure, not drawn to scale, is made up of Square A and Rectangles B and C. The area of Square A is 89 of the total area of Rectangles B and C. 14 of Square A is shaded. 14 of Rectangle B is shaded. 16 of Rectangle C is shaded. What fraction of the figure is shaded?
Level 3
The figure, not drawn to scale, is made up of Square A and Rectangles B and C. The area of Square A is 89 of the total area of Rectangles B and C. 14 of Square A is shaded. 14 of Rectangle B is shaded. 16 of Rectangle C is shaded. What fraction of the figure is shaded?
Image in this question is not available.
Level 3
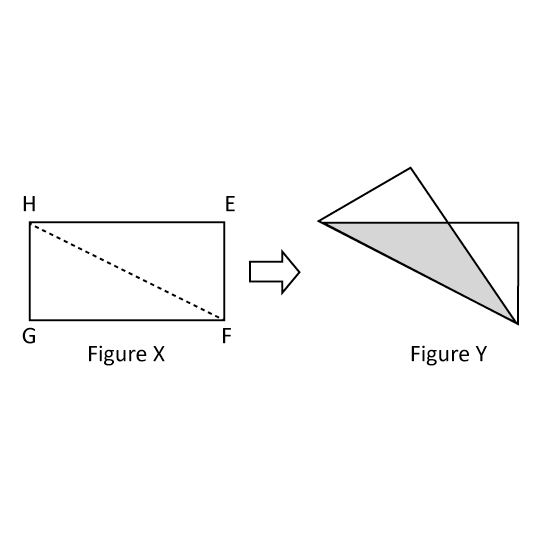
Figure 1 shows a rectangle EFGH. It is folded along EG to form Figure 2. The area of Figure 2 is 58 of the area of Figure 1. The area of the shaded part in Figure 2 is 36 cm2. Find the area of rectangle EFGH.
Level 3
Figure 1 shows a rectangle EFGH. It is folded along EG to form Figure 2. The area of Figure 2 is 58 of the area of Figure 1. The area of the shaded part in Figure 2 is 36 cm2. Find the area of rectangle EFGH.
Image in this question is not available.
Level 3
The figure is made of 2 quadrants and a rectangle. The rectangle measures 12 cm by 4 cm. Using the calculator value of π, find the area of the shaded part. Correct the answer to 2 decimal places.
Level 3
The figure is made of 2 quadrants and a rectangle. The rectangle measures 12 cm by 4 cm. Using the calculator value of π, find the area of the shaded part. Correct the answer to 2 decimal places.
Image in this question is not available.
Level 3
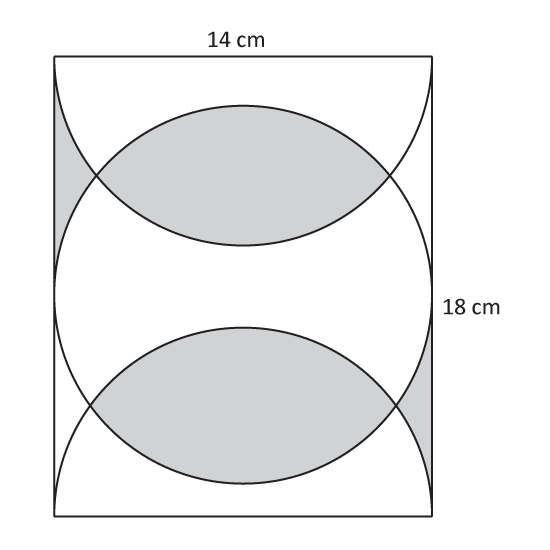
The figure consists of a rectangle, one circle and two semi-circles. The area of each overlapping shaded portion is 44 cm2. Find the total area of the shaded parts. (Take π = 227)
Level 3
The figure consists of a rectangle, one circle and two semi-circles. The area of each overlapping shaded portion is 44 cm2. Find the total area of the shaded parts. (Take π = 227)
Image in this question is not available.
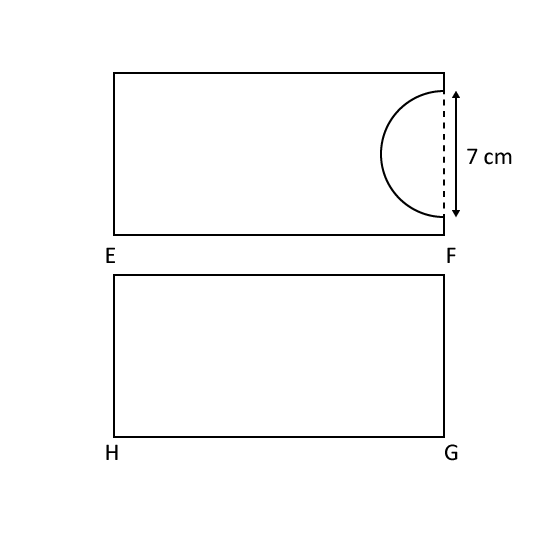
Level 3
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Level 3
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Image in this question is not available.