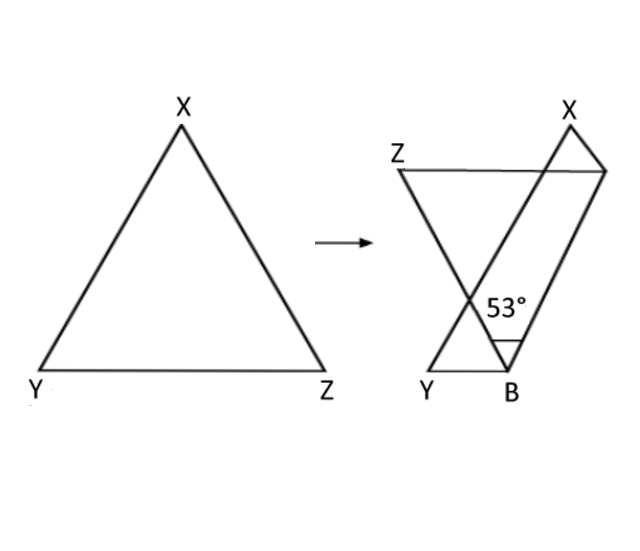Level 2
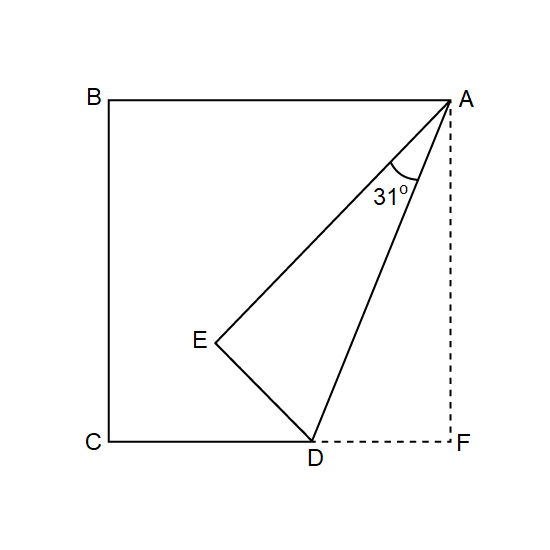
A square piece of paper is folded as shown in the figure.
- Find ∠ADE.
- Find ∠EDC.
Level 2
A square piece of paper is folded as shown in the figure.
- Find ∠ADE.
- Find ∠EDC.
Image in this question is not available.
Level 2
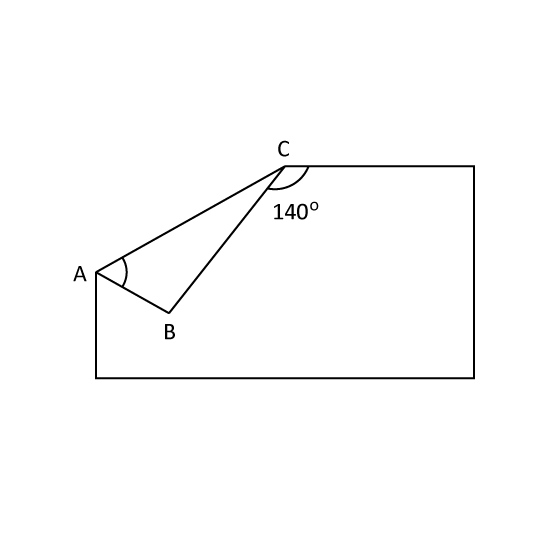
The figure shows a rectangular piece of paper folded at corner C. Find ∠BAC.
Level 2
The figure shows a rectangular piece of paper folded at corner C. Find ∠BAC.
Image in this question is not available.
Level 2 PSLE
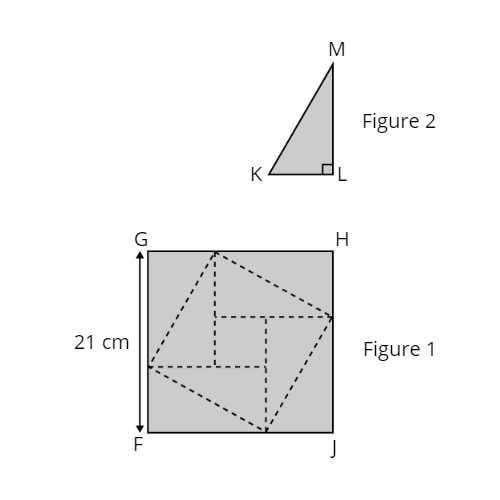
Anna has a square piece of paper FGHJ of side 21 cm. She cut along the dotted lines shown in Figure 1 to get one small square of area 9 cm2 and 8 identical right-angled triangles. Triangle KLM in Figure 2 is one such triangle. Find the length of KM.
Level 2 PSLE
Anna has a square piece of paper FGHJ of side 21 cm. She cut along the dotted lines shown in Figure 1 to get one small square of area 9 cm2 and 8 identical right-angled triangles. Triangle KLM in Figure 2 is one such triangle. Find the length of KM.
Image in this question is not available.
Level 2
An equilateral triangle, XYZ, is folded as shown in the figure. Find
- ∠BAZ
- ∠YBZ.
Level 2
An equilateral triangle, XYZ, is folded as shown in the figure. Find
- ∠BAZ
- ∠YBZ.
Image in this question is not available.
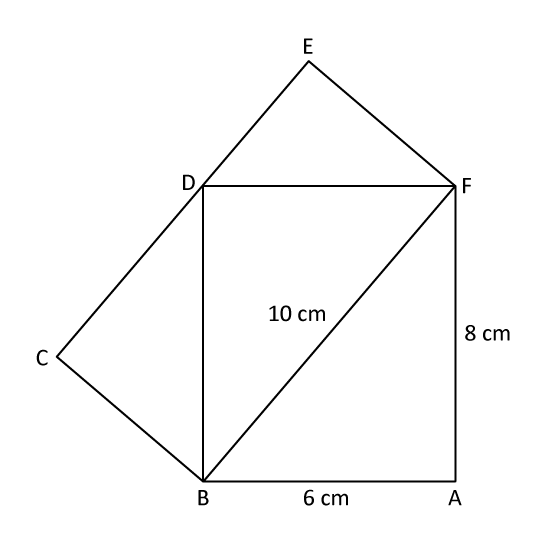
Level 2 PSLE
In the figure, ABDF and BCEF are rectangles and CDE is a straight line. AB = 6 cm, AF = 8 cm and BF = 10 cm. Find the length of BC.
Level 2 PSLE
In the figure, ABDF and BCEF are rectangles and CDE is a straight line. AB = 6 cm, AF = 8 cm and BF = 10 cm. Find the length of BC.
Image in this question is not available.
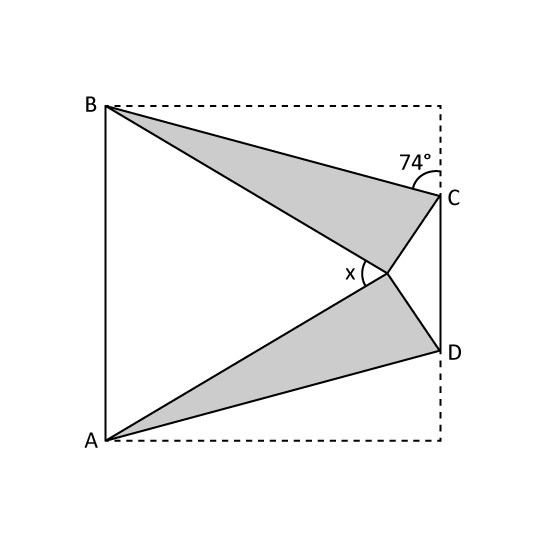
Level 2 PSLE
A rectangular piece of paper is folded to form a trapezium ABCD. The two shaded triangles are identical. Find ∠x.
Level 2 PSLE
A rectangular piece of paper is folded to form a trapezium ABCD. The two shaded triangles are identical. Find ∠x.
Image in this question is not available.
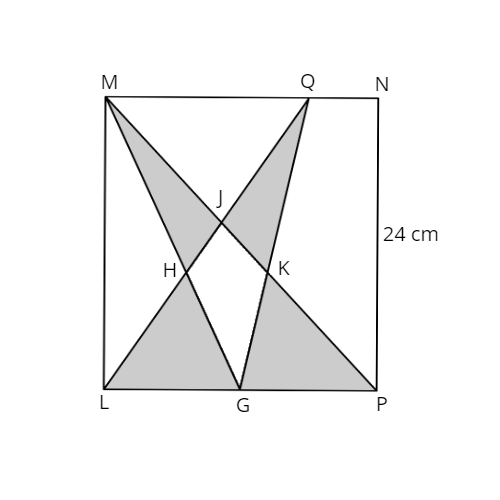
Level 2
The figure is not drawn to scale. Given that GL = GP, NM = 18 cm and the area of GHJK is 45 cm2, find the area of the shaded parts.
Level 2
The figure is not drawn to scale. Given that GL = GP, NM = 18 cm and the area of GHJK is 45 cm2, find the area of the shaded parts.
Image in this question is not available.
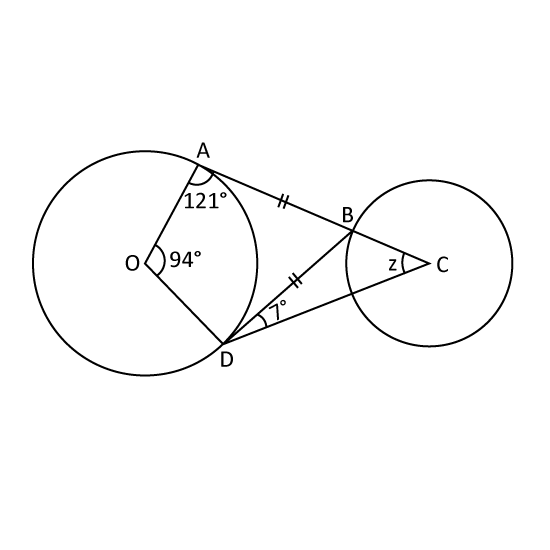
Level 2
In the figure, not drawn to scale, O and C are the centres of the circles. AC is a straight line. Find ∠z.
Level 2
In the figure, not drawn to scale, O and C are the centres of the circles. AC is a straight line. Find ∠z.
Image in this question is not available.
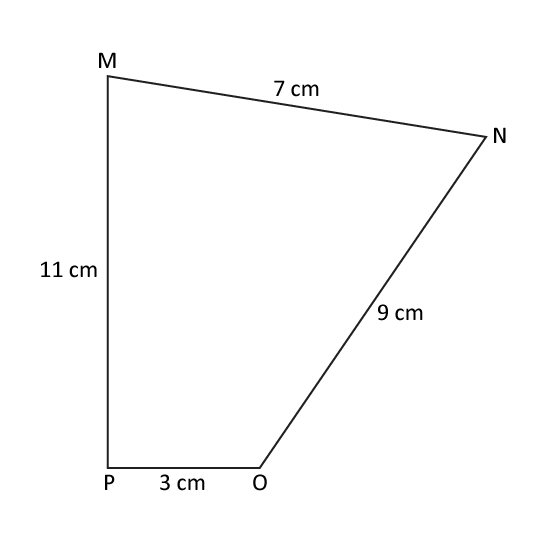
Level 2 PSLE
In the figure, MN = 7 cm, NO = 9 cm, OP = 3 cm and PM = 11 cm. ∠MNO and ∠OPM are right angles. Find the area of the figure MNOP.
Level 2 PSLE
In the figure, MN = 7 cm, NO = 9 cm, OP = 3 cm and PM = 11 cm. ∠MNO and ∠OPM are right angles. Find the area of the figure MNOP.
Image in this question is not available.
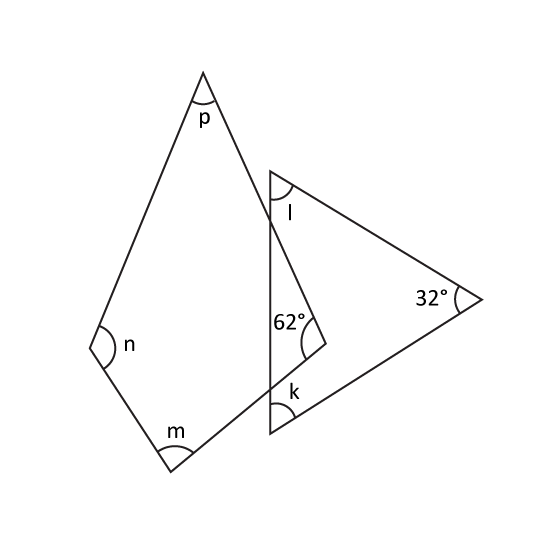
Level 2
Find the sum of ∠m, ∠n, ∠p, ∠l and ∠k.
Level 2
Find the sum of ∠m, ∠n, ∠p, ∠l and ∠k.
Image in this question is not available.
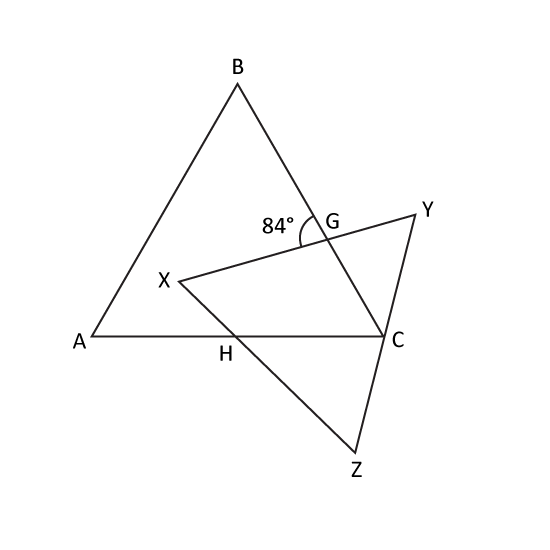
Level 2
In the figure, ABC and XYZ are equilateral triangles and ∠BGX = 84°. Find ∠CHZ.
Level 2
In the figure, ABC and XYZ are equilateral triangles and ∠BGX = 84°. Find ∠CHZ.
Image in this question is not available.
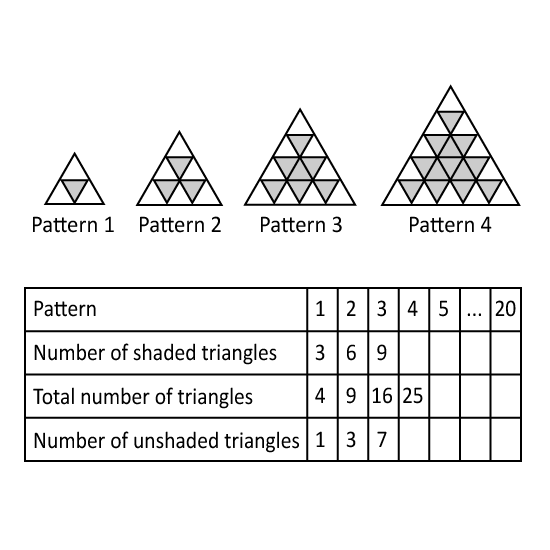
Level 3
Some patterns of shaded and unshaded small triangles is given. The unshaded triangles are those which have at least one side on the edge of the big triangle. All of the other small triangles are shaded. The table below shows numbers of small triangles.
- Find the total number of triangles in Pattern 80.
- Find the number of shaded triangles in Pattern 40.
- Find the number of unshaded triangles in Pattern 50.
Level 3
Some patterns of shaded and unshaded small triangles is given. The unshaded triangles are those which have at least one side on the edge of the big triangle. All of the other small triangles are shaded. The table below shows numbers of small triangles.
- Find the total number of triangles in Pattern 80.
- Find the number of shaded triangles in Pattern 40.
- Find the number of unshaded triangles in Pattern 50.
Image in this question is not available.
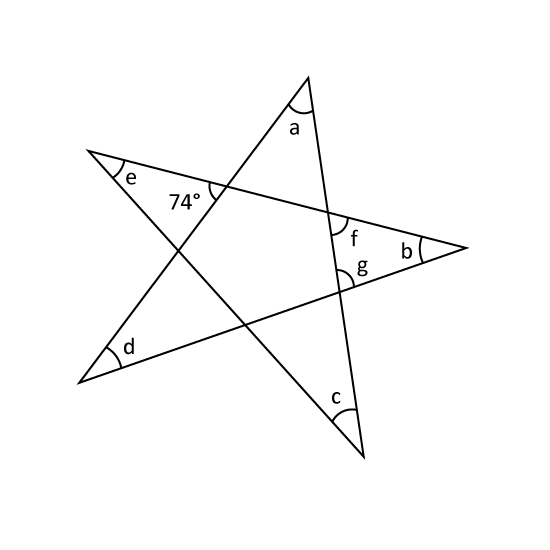
Level 2
The figure, not drawn to scale, shows a regular 5-point star and ∠a = ∠b = ∠c = ∠d = ∠e.
- Express ∠f as a sum of two angles. Give the answers in equation. (Eg ∠a + ∠b)
- lf ∠e = 32°, find ∠f.
Level 2
The figure, not drawn to scale, shows a regular 5-point star and ∠a = ∠b = ∠c = ∠d = ∠e.
- Express ∠f as a sum of two angles. Give the answers in equation. (Eg ∠a + ∠b)
- lf ∠e = 32°, find ∠f.
Image in this question is not available.
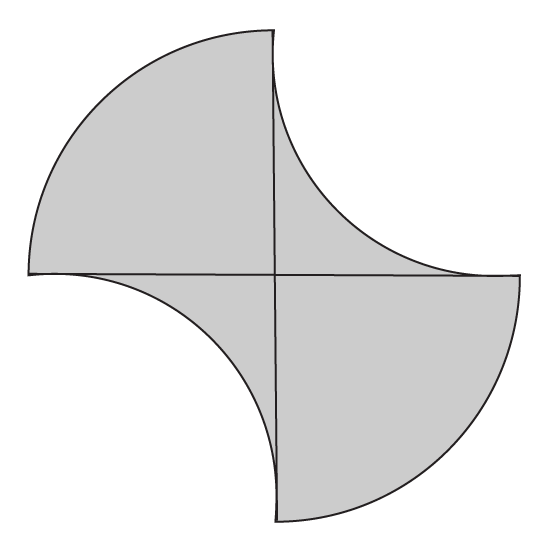
Level 2
The shaded figure is made up of 4 quarter arcs of radius 12 cm. Find its area.
(Take π = 3.14)
Level 2
The shaded figure is made up of 4 quarter arcs of radius 12 cm. Find its area.
(Take π = 3.14)
Image in this question is not available.
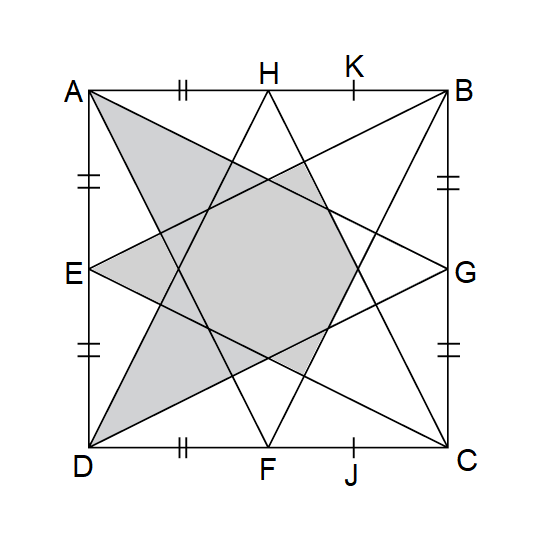
Level 2
The figure is formed using four identical isosceles triangles. AGD, AFB, BEC and CHD. ABCD is a square where E, F, G and H are midpoints of its sides. Given FJ = CJ, HK = BK and AD = 14 cm, find the total area of the shaded parts.
Level 2
The figure is formed using four identical isosceles triangles. AGD, AFB, BEC and CHD. ABCD is a square where E, F, G and H are midpoints of its sides. Given FJ = CJ, HK = BK and AD = 14 cm, find the total area of the shaded parts.
Image in this question is not available.
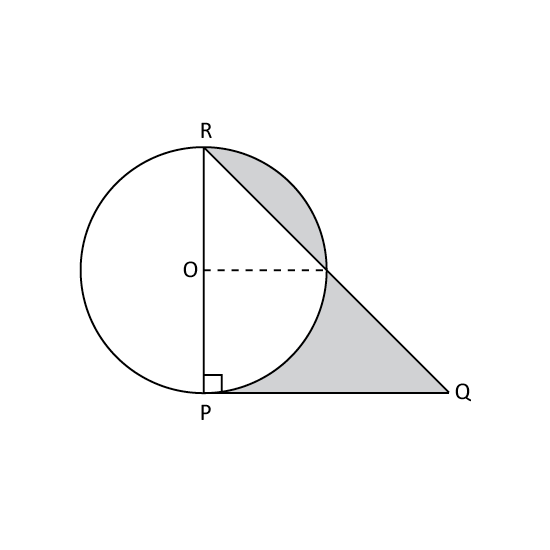
Level 2
The figure is formed by a circle and an isosceles triangle where PQ = PR. The radius of the circle is 14 cm. Find the area of the shaded part. (Take π = 227)
Level 2
The figure is formed by a circle and an isosceles triangle where PQ = PR. The radius of the circle is 14 cm. Find the area of the shaded part. (Take π = 227)
Image in this question is not available.
Level 2
Tony drove a distance of 15 km in 10 minutes.
- What was his speed in km/h?
- How long will it take him to cover 360 km at this speed? Express the answer in hours.
3 m
Image in this question is not available.
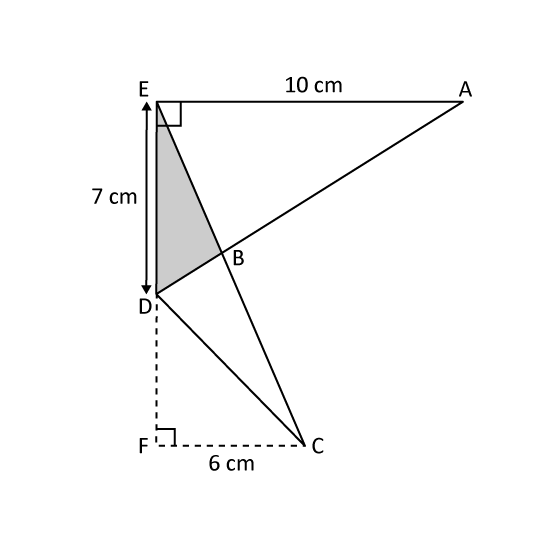
Level 3 PSLE
Figure ABCDE has an area of 42 cm2. ABD and CBE are straight lines. Find the area of the shaded triangle BDE.
Level 3 PSLE
Figure ABCDE has an area of 42 cm2. ABD and CBE are straight lines. Find the area of the shaded triangle BDE.
Image in this question is not available.
Level 2
A van covers a distance of 45 km in 25 minutes.
- At what speed is it travelling?
- How long will it take to cover a distance of 36 km?
3 m
Image in this question is not available.
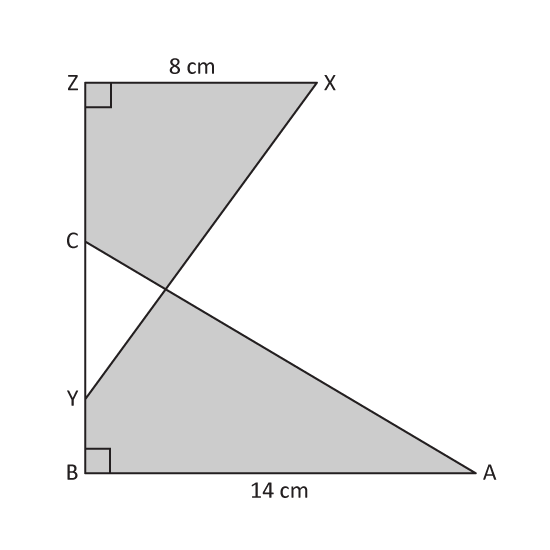
Level 3 PSLE
In the figure, ABC and XZY are identical right-angled triangles. The total area of the shaded parts is 96 cm2. Find the area of the unshaded part.
Level 3 PSLE
In the figure, ABC and XZY are identical right-angled triangles. The total area of the shaded parts is 96 cm2. Find the area of the unshaded part.
Image in this question is not available.