Level 1
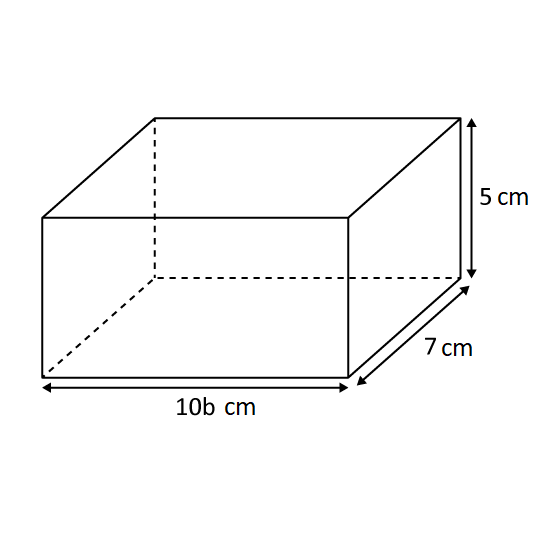
Find the volume of the cuboid.
Level 1
Find the volume of the cuboid.
Image in this question is not available.
Level 1 PSLE
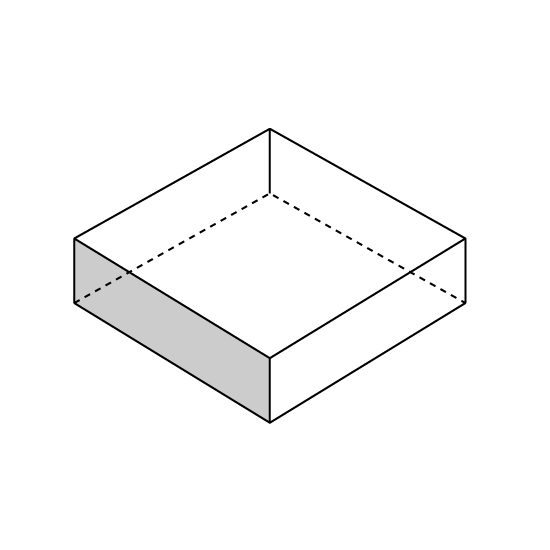
The figure shows a cuboid with a square base and a height of 2 cm.
The area of the shaded face is 20 cm2.
What is the volume of the cuboid?
Level 1 PSLE
The figure shows a cuboid with a square base and a height of 2 cm.
The area of the shaded face is 20 cm2.
What is the volume of the cuboid?
Image in this question is not available.
Level 1 PSLE
Is the following the net of the cuboid? Give your answer in number. (Eg Yes = 1; No = 2)
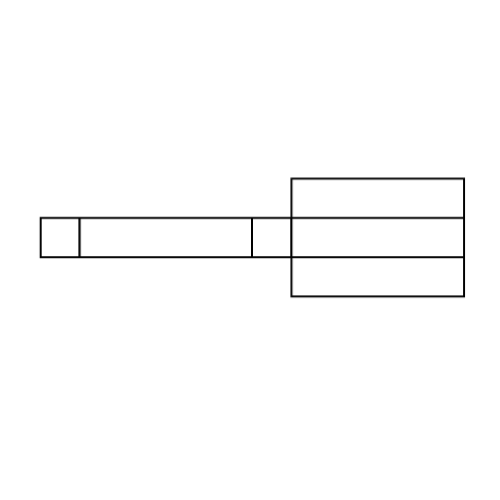
Level 1 PSLE
Is the following the net of the cuboid? Give your answer in number. (Eg Yes = 1; No = 2)
Image in this question is not available.
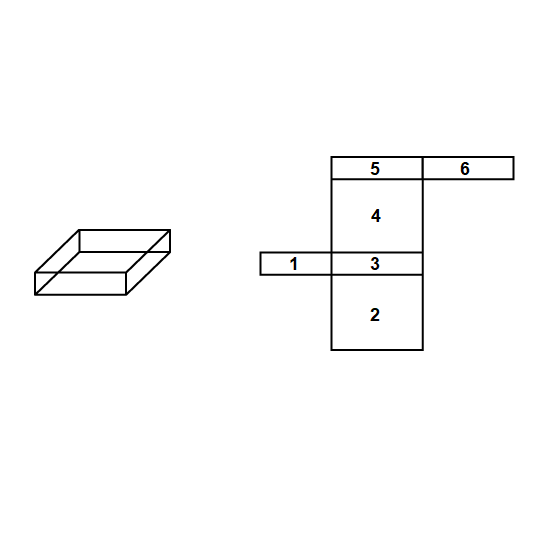
Level 1
The net drawn for the cuboid is incorrect. Which part does not fit? Give your answer in number. (Eg 1)
Level 1
The net drawn for the cuboid is incorrect. Which part does not fit? Give your answer in number. (Eg 1)
Image in this question is not available.
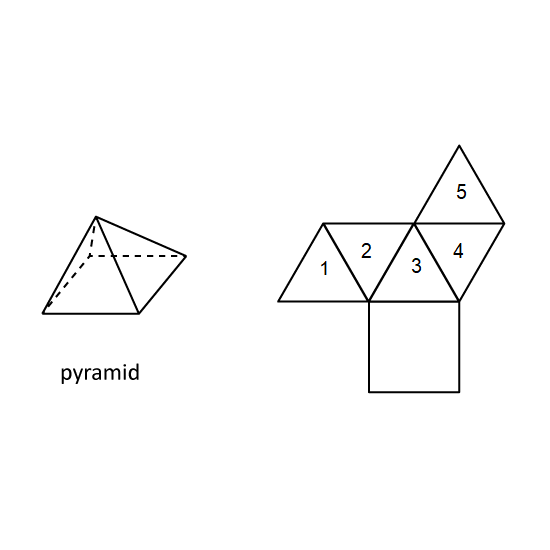
Level 1 PSLE
The net drawn for the pyramid is incorrect. Which part does not fit? Give your answer in number. (Eg 1)
Level 1 PSLE
The net drawn for the pyramid is incorrect. Which part does not fit? Give your answer in number. (Eg 1)
Image in this question is not available.
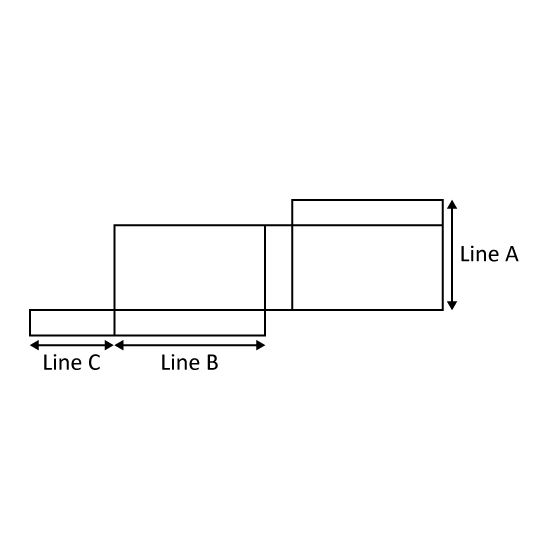
Level 2
The figure shows the net of a cuboid not drawn to scale. Line A is 50 cm. Line B is 40 cm. Line C is 35 cm. Find the volume of the cuboid.
Level 2
The figure shows the net of a cuboid not drawn to scale. Line A is 50 cm. Line B is 40 cm. Line C is 35 cm. Find the volume of the cuboid.
Image in this question is not available.
Level 2
The length, breadth and height of a cuboid are in the ratio 8 : 5 : 2. If the length of the cuboid is 30 cm longer than its height, find its volume.
2 m
Image in this question is not available.
Level 1
What is the maximum number of cubes of edge 6 cm that can be cut from a foam cuboid, 67 cm by 36 cm by 27 cm?
2 m
Image in this question is not available.
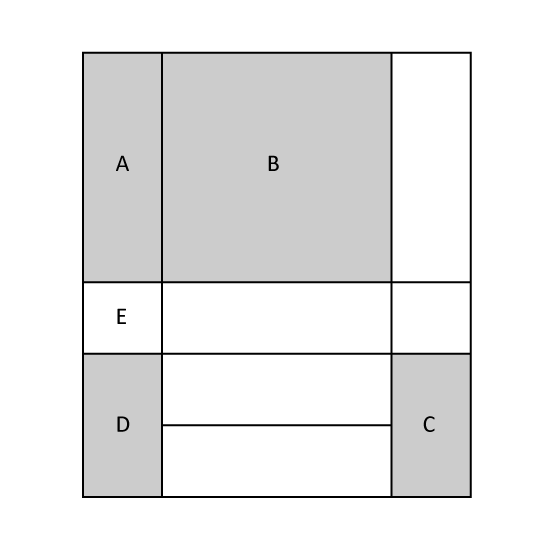
Level 2
The figure shows a piece of paper. When the shaded rectangles A, C, D and square B is cut out, the remaining parts form the net of a cuboid. Area E is a square. Given that the area of A is 18 cm2 and the area of B is 81 cm2, find the volume of the cuboid.
Level 2
The figure shows a piece of paper. When the shaded rectangles A, C, D and square B is cut out, the remaining parts form the net of a cuboid. Area E is a square. Given that the area of A is 18 cm2 and the area of B is 81 cm2, find the volume of the cuboid.
Image in this question is not available.
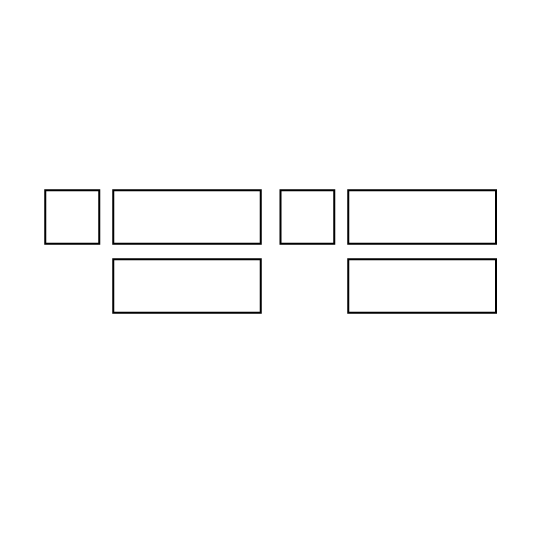
Level 2
The figure shows cardboard pieces used to form the net of a cuboid. The area of each square piece is 25 cm2 and the area of each rectangular piece is 40 cm2. Find the volume of the cuboid.
Level 2
The figure shows cardboard pieces used to form the net of a cuboid. The area of each square piece is 25 cm2 and the area of each rectangular piece is 40 cm2. Find the volume of the cuboid.
Image in this question is not available.
Level 2
A cuboid has a square face of area 49 cm2. The ratio of its length to its breadth is 9 : 7. Find its volume.
Level 2
A cuboid has a square face of area 49 cm2. The ratio of its length to its breadth is 9 : 7. Find its volume.
Image in this question is not available.
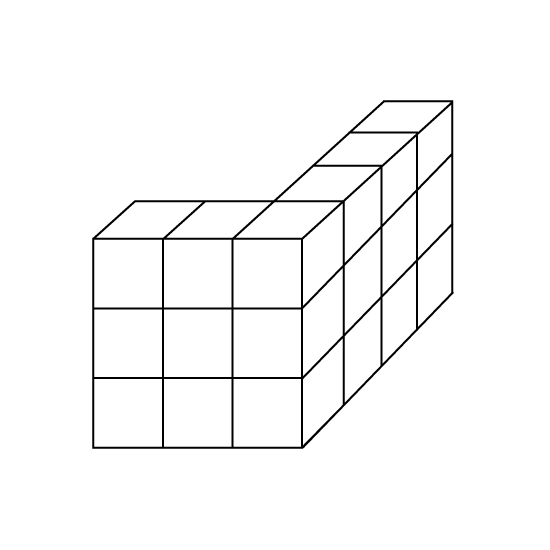
Level 2 PSLE Jenson glued 18 cubes of side 1 cm to form the solid shown.
- Jenson painted the whole solid, including the base. What was the total painted area?
- Jenson added some cubes of side 1 cm to the solid to form a cuboid 3 cm by 5 cm by 5 cm. How many cubes did he add?
Level 2 PSLE Jenson glued 18 cubes of side 1 cm to form the solid shown.
- Jenson painted the whole solid, including the base. What was the total painted area?
- Jenson added some cubes of side 1 cm to the solid to form a cuboid 3 cm by 5 cm by 5 cm. How many cubes did he add?
Image in this question is not available.
Level 1
What is the maximum number of 3 cm cubes that can be filled into a 12 cm by 9 cm by 7 cm cuboid?
2 m
Image in this question is not available.
Level 2
Find the maximum number of cubes of edge 3 cm that can be cut from a foam cuboid, 27 cm by 24 cm by 18 cm.
2 m
Image in this question is not available.
Level 2 PSLE
Jamie formed two cuboids with unit cubes. The length, breadth and height of the bigger cuboid are 2 times those of the smaller cuboid. She used 348 unit cubes to form the smaller cuboid.
How many unit cubes did she use to form the larger cuboid?
2 m
Image in this question is not available.
Level 2
A rectangular tank has a base area of 50 cm2. It is half filled with water. If 4 bottles of water are poured into the tank, 250 mℓ of water will overflow. If 3 bottles of water are poured into the tank, 100 mℓ of water will overflow. Find the height of the tank.
2 m
Image in this question is not available.
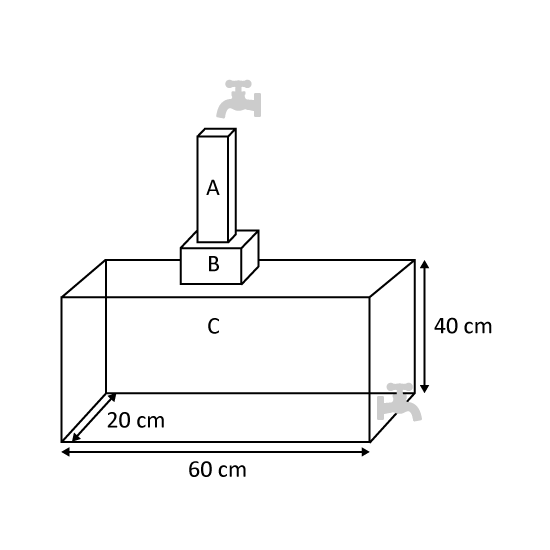
Level 3
The figure shows a tank made up of 3 sections. Cuboid A with a square base of side 4 cm and height 30 cm. Cube B with a side of 12 cm. Cuboid C that is 60 cm by 20 cm by 40 cm. Water from a tap above flows down at a rate of 1.2 litres per minute while water is drained out from the bottom at a rate of 1 litre per minute. How long did it take to fill up the tank to a height of 66 cm from the base? Give the answer in minutes correct to nearest whole number.
Level 3
The figure shows a tank made up of 3 sections. Cuboid A with a square base of side 4 cm and height 30 cm. Cube B with a side of 12 cm. Cuboid C that is 60 cm by 20 cm by 40 cm. Water from a tap above flows down at a rate of 1.2 litres per minute while water is drained out from the bottom at a rate of 1 litre per minute. How long did it take to fill up the tank to a height of 66 cm from the base? Give the answer in minutes correct to nearest whole number.
Image in this question is not available.
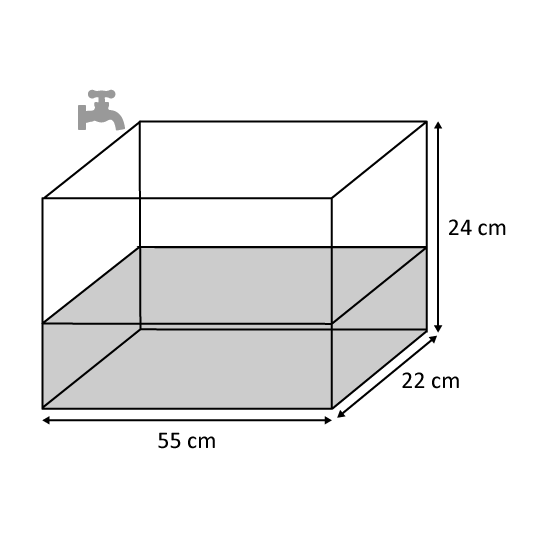
Level 3
The figure shows a rectangular tank measuring 55 cm by 22 cm by 24 cm. It was 13 filled with water at first. Dylan turned on a tap and let water flow into the tank at a rate of 1.36ℓ per minute. After 15 minutes, he turned off the tap. How much water had overflowed? (Express the answer in ℓ.)
Level 3
The figure shows a rectangular tank measuring 55 cm by 22 cm by 24 cm. It was 13 filled with water at first. Dylan turned on a tap and let water flow into the tank at a rate of 1.36ℓ per minute. After 15 minutes, he turned off the tap. How much water had overflowed? (Express the answer in ℓ.)
Image in this question is not available.
Level 3
Shemy placed three empty tanks side by side. The smallest tank has a crack at its side and the base area of each tank is 16 cm2. After she turned on the tap for 64 minutes, the height of the water in the smallest tank became 6 cm although 0.5 mℓ of water is leaking out of the crack per minute. Find the rate of flow of water from the tap. Give the answer in mℓ/min.
Level 3
Shemy placed three empty tanks side by side. The smallest tank has a crack at its side and the base area of each tank is 16 cm2. After she turned on the tap for 64 minutes, the height of the water in the smallest tank became 6 cm although 0.5 mℓ of water is leaking out of the crack per minute. Find the rate of flow of water from the tap. Give the answer in mℓ/min.
Image in this question is not available.
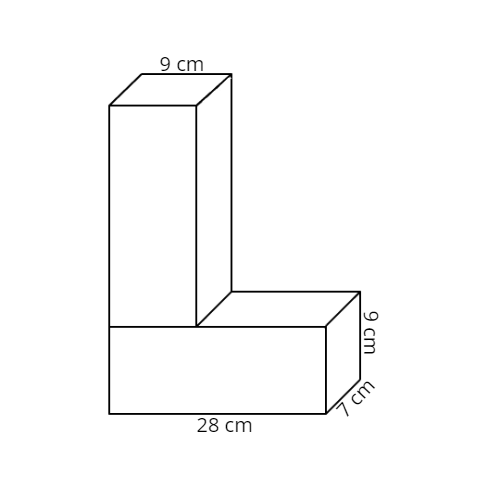
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Level 3 Oscar had two identical wooden cuboid measuring 28 cm by 7 cm by 9 cm. He glued them together to form a solid as shown. He then painted the whole solid in white paint. After that, he cut the solid into 1-cm cubes.
- How many 1-cm cubes did he get?
- How many 1-cm cubes had none of its faces painted white?
Image in this question is not available.