Level 3
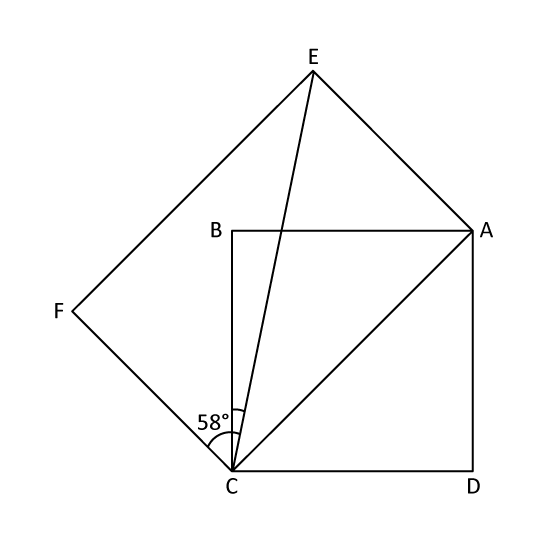
In the figure, ABCD is a square and AEFC is a rectangle. EC is a straight line and ∠ECF = 58°. Find ∠ECB.
Level 3
In the figure, ABCD is a square and AEFC is a rectangle. EC is a straight line and ∠ECF = 58°. Find ∠ECB.
Image in this question is not available.
Level 3
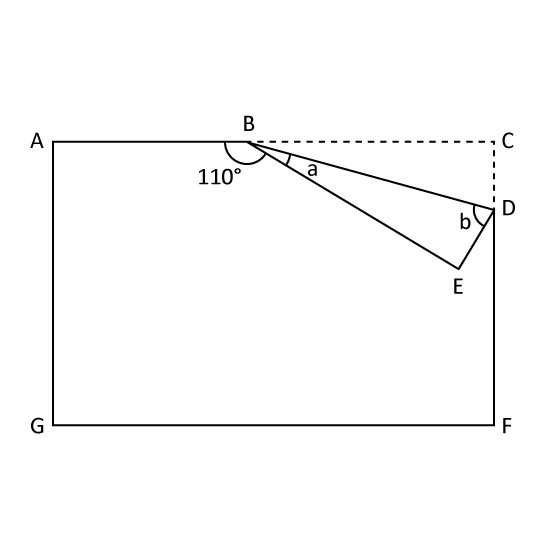
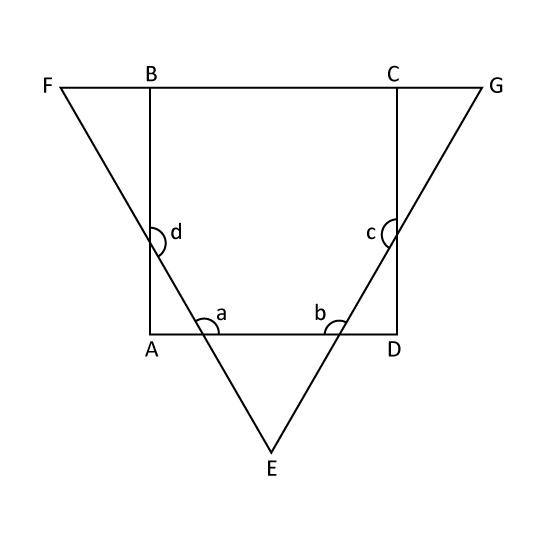
A rectangular piece of paper is folded to form the diagram.
- Find ∠a.
- Find ∠b.
Level 3
A rectangular piece of paper is folded to form the diagram.
- Find ∠a.
- Find ∠b.
Image in this question is not available.
Level 3
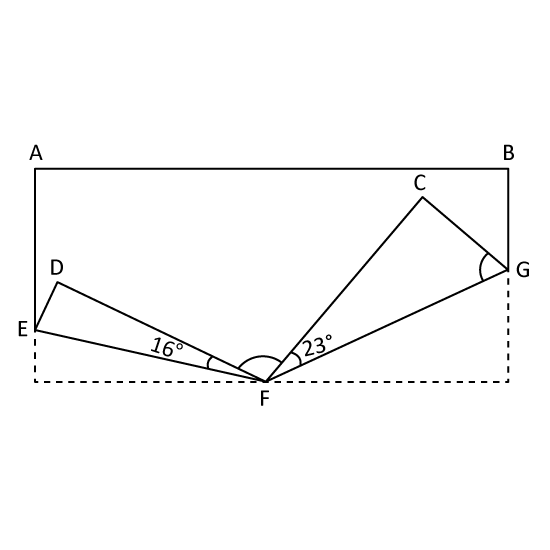
ABCD is a rectangular piece of paper. Corners C and D are folded upwards as shown. ∠CFG = 23° and ∠DFE = 16 °
- Find ∠CGF
- Find ∠DFC
Level 3
ABCD is a rectangular piece of paper. Corners C and D are folded upwards as shown. ∠CFG = 23° and ∠DFE = 16 °
- Find ∠CGF
- Find ∠DFC
Image in this question is not available.
Level 3
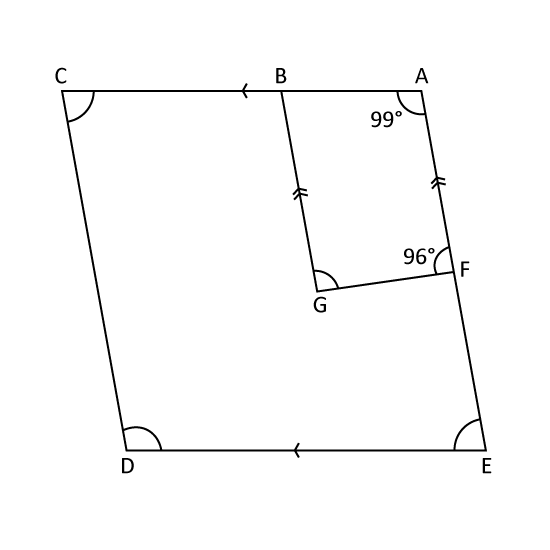
In the figure, AC is parallel to ED and AF is parallel to BG. AFE is a straight line, ∠AFG = 96°. ∠FAB = 99° and the sum of ∠BCD and ∠DEF is 150°. Find
- ∠FGB
- ∠EDC
Level 3
In the figure, AC is parallel to ED and AF is parallel to BG. AFE is a straight line, ∠AFG = 96°. ∠FAB = 99° and the sum of ∠BCD and ∠DEF is 150°. Find
- ∠FGB
- ∠EDC
Image in this question is not available.
Level 3
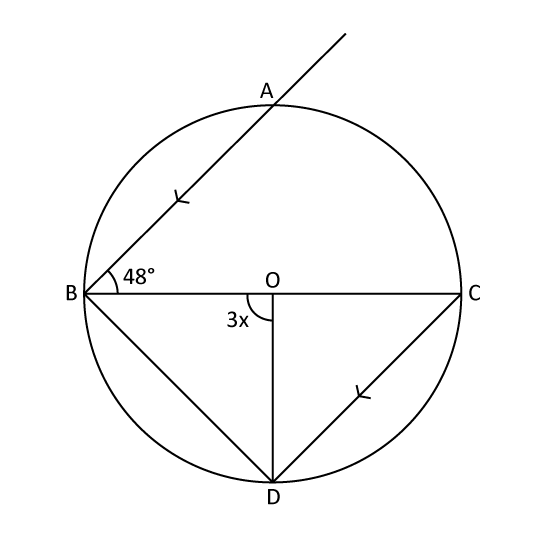
In the figure, O is the centre of the circle. ∠ABD is 90°. Find ∠x.
Level 3
In the figure, O is the centre of the circle. ∠ABD is 90°. Find ∠x.
Image in this question is not available.
Level 3
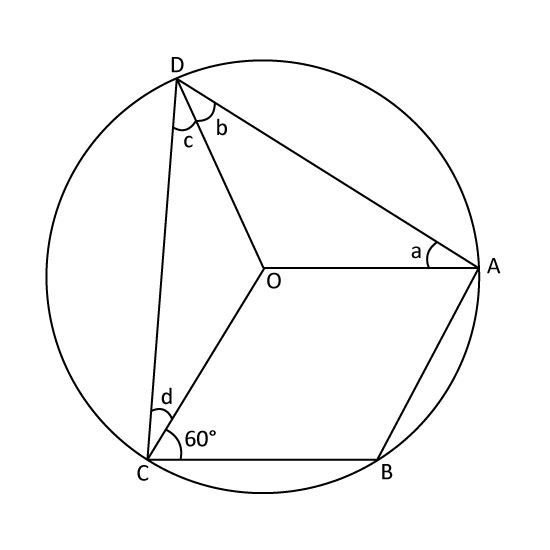
In the figure, O is the centre of the circle and OABC is a rhombus. Find the value of ∠a + ∠b + ∠c + ∠d.
Level 3
In the figure, O is the centre of the circle and OABC is a rhombus. Find the value of ∠a + ∠b + ∠c + ∠d.
Image in this question is not available.
Level 3
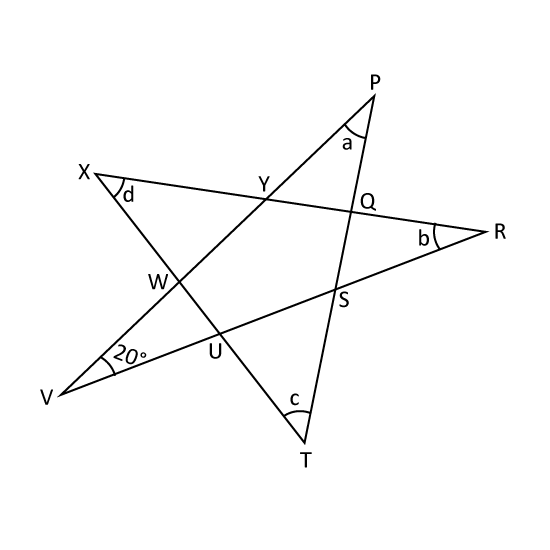
In the figure, PQST, PYWV, RQYX, XWUT and RSUV are straight lines. Find the value of ∠a + ∠b + ∠c + ∠d.
Level 3
In the figure, PQST, PYWV, RQYX, XWUT and RSUV are straight lines. Find the value of ∠a + ∠b + ∠c + ∠d.
Image in this question is not available.
Level 3
In the figure, JKLM is a parallelogram. Find ∠b.
Level 3
In the figure, JKLM is a parallelogram. Find ∠b.
Image in this question is not available.
Level 3
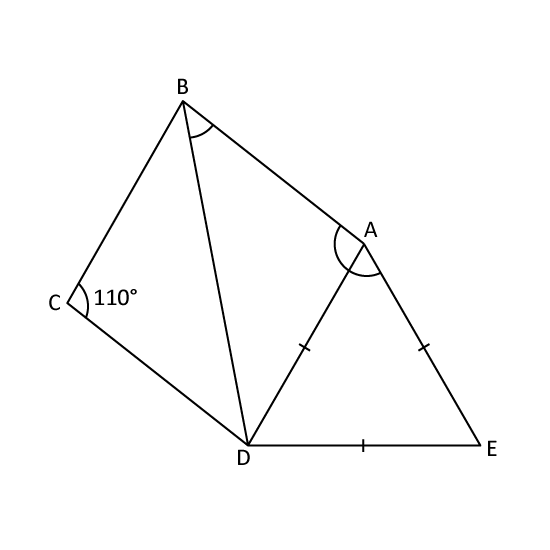
ABCD is a rhombus. ADE is an equilateral triangle. Find
- ∠EAB
- ∠ABD
Level 3
ABCD is a rhombus. ADE is an equilateral triangle. Find
- ∠EAB
- ∠ABD
Image in this question is not available.
Level 3
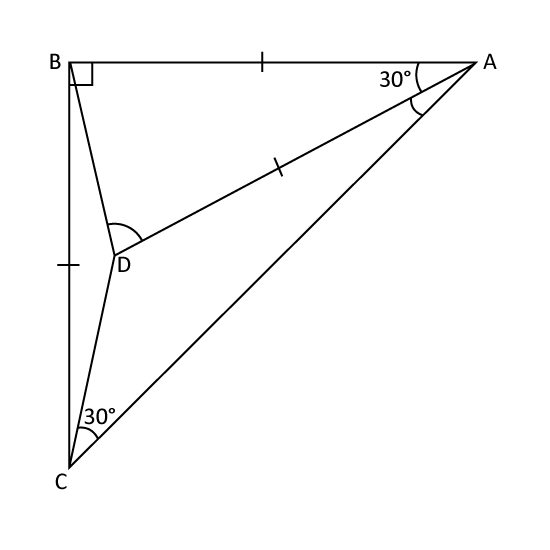
In the diagram shown, ABC is a right-angled triangle and AB = BC = AD. Find
- ∠DAC
- ∠ADB
Level 3
In the diagram shown, ABC is a right-angled triangle and AB = BC = AD. Find
- ∠DAC
- ∠ADB
Image in this question is not available.
Level 3
In the figure, EFG is an equilateral triangle, ABCD is a square and FBCG is a straight line. Find the sum of ∠a, ∠b, ∠c and ∠d.
Level 3
In the figure, EFG is an equilateral triangle, ABCD is a square and FBCG is a straight line. Find the sum of ∠a, ∠b, ∠c and ∠d.
Image in this question is not available.
Level 3
In the figure, ABCD is a rhombus and ACE is a straight line. Find ∠BEC.
Level 3
In the figure, ABCD is a rhombus and ACE is a straight line. Find ∠BEC.
Image in this question is not available.
Level 3
In the figure, not drawn to scale, ABC, BFG, BDE, ADF are straight lines. Given that ∠CBF is twice the size of ∠FBD. Find ∠BAF.
Level 3
In the figure, not drawn to scale, ABC, BFG, BDE, ADF are straight lines. Given that ∠CBF is twice the size of ∠FBD. Find ∠BAF.
Image in this question is not available.
Level 3
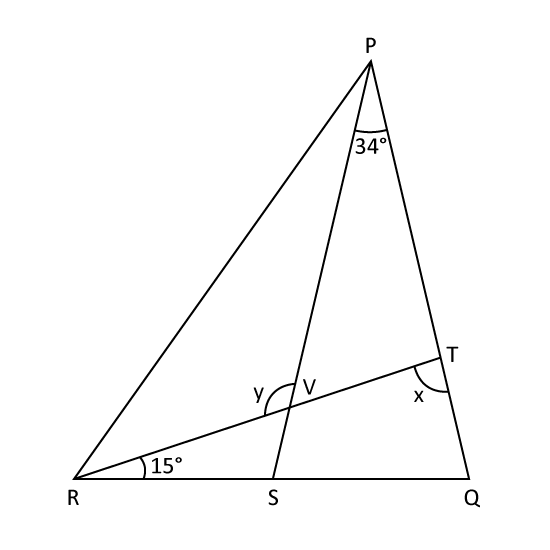
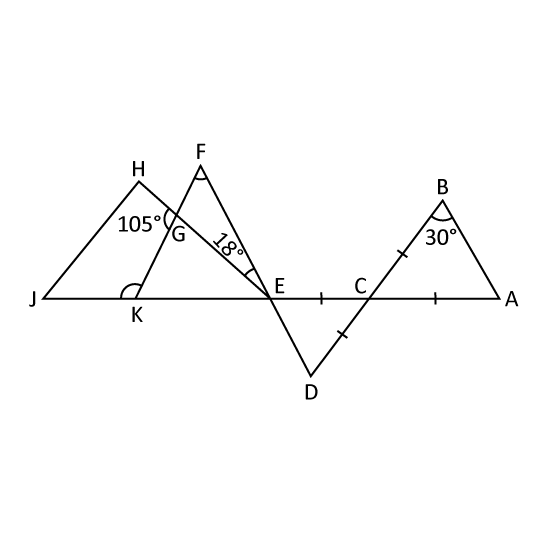
In the figure, PQ = PS, ∠QPS = 34° and ∠TRS = 15°. Find
- ∠x
- ∠y
Level 3
In the figure, PQ = PS, ∠QPS = 34° and ∠TRS = 15°. Find
- ∠x
- ∠y
Image in this question is not available.
Level 3
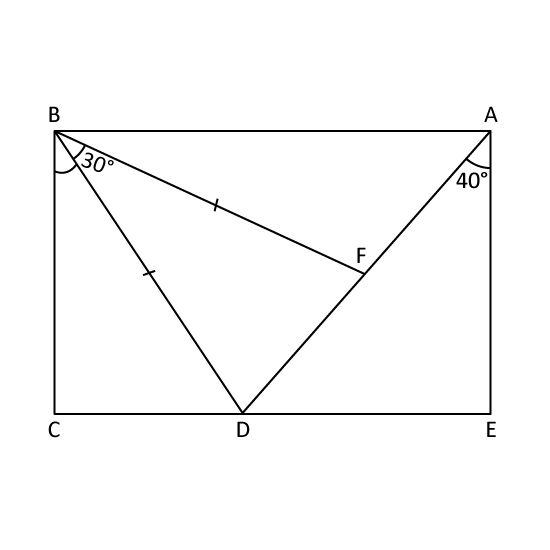
ABCE is a rectangle. Given that FBD is an isosceles triangle, find ∠DBC.
Level 3
ABCE is a rectangle. Given that FBD is an isosceles triangle, find ∠DBC.
Image in this question is not available.
Level 3
In the figure, ABC and CDE are isosceles triangles where AC = BC and CD = CE. Given that DF, EH and AJ are straight lines, find
- ∠GKJ
- ∠EFK
Level 3
In the figure, ABC and CDE are isosceles triangles where AC = BC and CD = CE. Given that DF, EH and AJ are straight lines, find
- ∠GKJ
- ∠EFK
Image in this question is not available.
Level 3
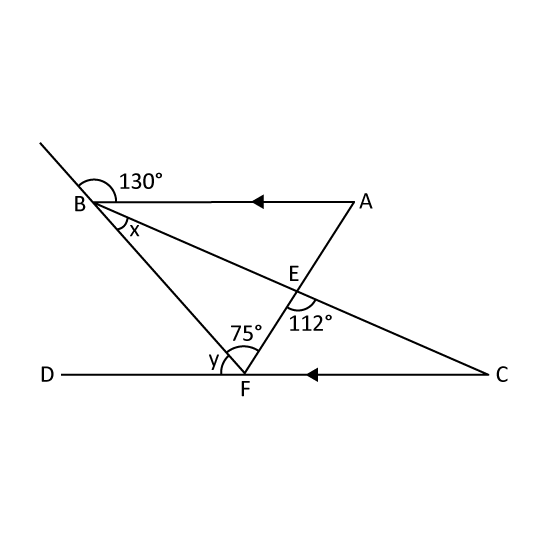
Given the figure, find
- ∠y
- ∠x
Level 3
Given the figure, find
- ∠y
- ∠x
Image in this question is not available.
Level 3
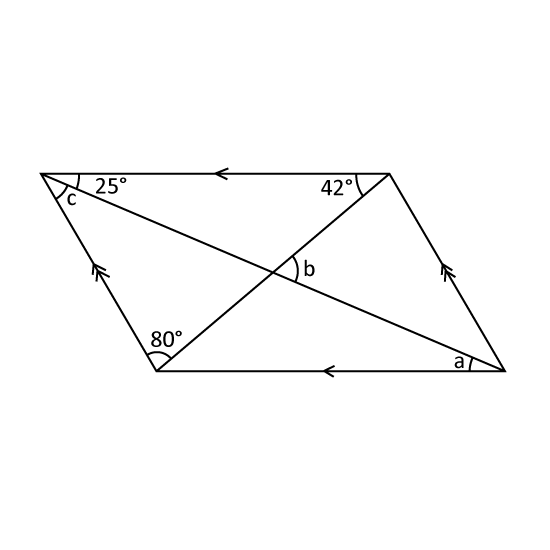
The figure shows a parallelogram. Find
- ∠a
- ∠b
- ∠c
Level 3
The figure shows a parallelogram. Find
- ∠a
- ∠b
- ∠c
Image in this question is not available.
Level 3
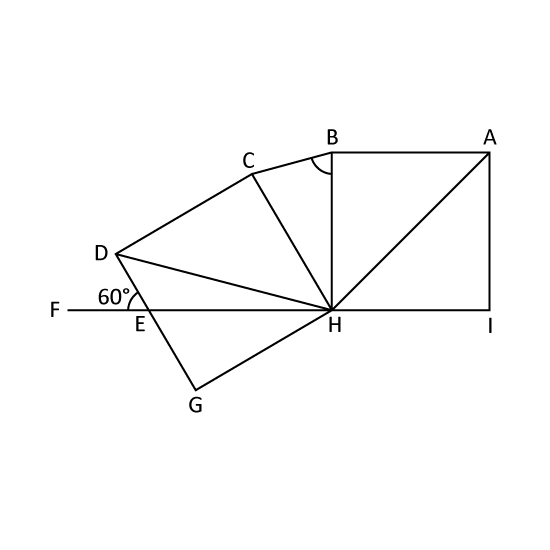
ABHI and CDGH are identical squares. Given that ∠DEF = 60° and FI is a straight line, find ∠HBC.
Level 3
ABHI and CDGH are identical squares. Given that ∠DEF = 60° and FI is a straight line, find ∠HBC.
Image in this question is not available.
Level 3
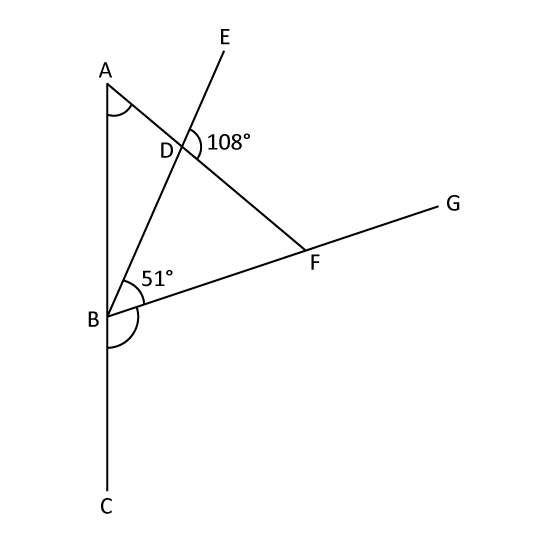
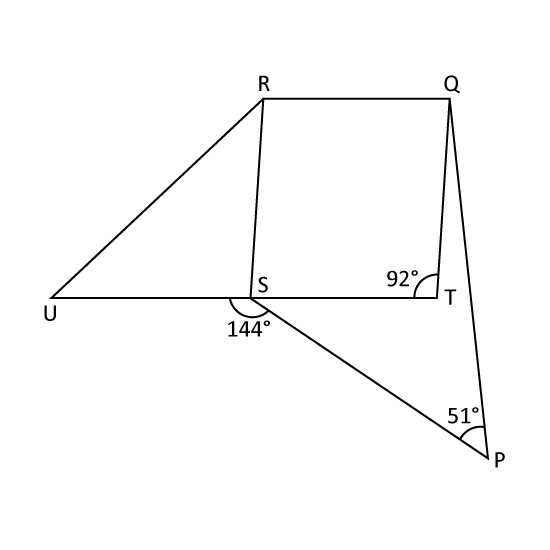
In the figure, RSU is a triangle with SU = SR, while QRST is a parallelogram and TSU is a straight line. Given ∠STQ = 92°, ∠PSU = 144° and ∠QPS = 51°, find
- ∠SRU
- ∠PSR
Level 3
In the figure, RSU is a triangle with SU = SR, while QRST is a parallelogram and TSU is a straight line. Given ∠STQ = 92°, ∠PSU = 144° and ∠QPS = 51°, find
- ∠SRU
- ∠PSR
Image in this question is not available.