TRY FOR FREE
Level 3 PSLE
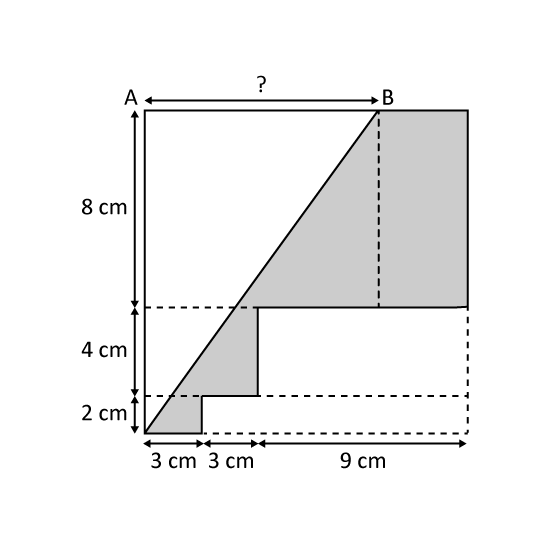
The figure is made up of three rectangles. A straight line drawn across the rectangles, divides the figure into two parts: shaded and unshaded.
- The perimeter of the shaed part is 8 cm longer than the perimeter of the unshaded part. What is the length of AB?
- What is the area of the shaded part?
Level 3 PSLE
The figure is made up of three rectangles. A straight line drawn across the rectangles, divides the figure into two parts: shaded and unshaded.
- The perimeter of the shaed part is 8 cm longer than the perimeter of the unshaded part. What is the length of AB?
- What is the area of the shaded part?
Image in this question is not available.
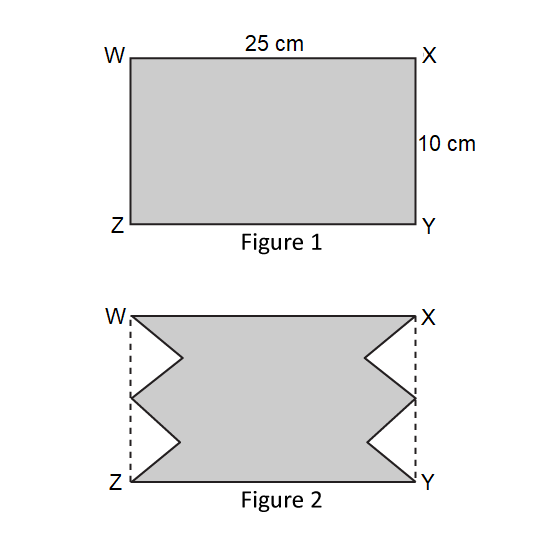
Level 3 PSLE In Figure 1, WXYZ is a rectangular piece of paper. After 4 identical triangles are cut out from the paper, the remaining paper is shown in Figure 2. The area of the remaining paper is 186 cm
2.
- What is the area of each triangle that was cut out?
- The perimeter of Figure 2 is 36 cm longer than the perimeter of Figure 1. What is the perimeter of each triangle?
Level 3 PSLE In Figure 1, WXYZ is a rectangular piece of paper. After 4 identical triangles are cut out from the paper, the remaining paper is shown in Figure 2. The area of the remaining paper is 186 cm
2.
- What is the area of each triangle that was cut out?
- The perimeter of Figure 2 is 36 cm longer than the perimeter of Figure 1. What is the perimeter of each triangle?
Image in this question is not available.
Level 3
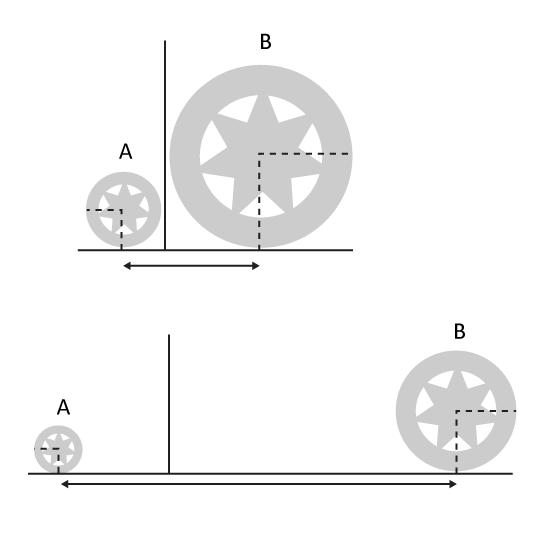
This figure is not drawn to scale. Wheel A and Wheel B are touching a vertical plastic sheet. The ratio of the radius of the small wheel A to the radius of the big wheel B is 2 : 5. The total radii of Wheel A and Wheel B is 196 cm. Both wheels are rolled out in opposite direction shown until they are 2660 cm apart. The two wheels need to make the same number of revolutions. How many revolutions does each wheel make assuming that each wheel must make a complete revolution? (Take π = 227)
Level 3
This figure is not drawn to scale. Wheel A and Wheel B are touching a vertical plastic sheet. The ratio of the radius of the small wheel A to the radius of the big wheel B is 2 : 5. The total radii of Wheel A and Wheel B is 196 cm. Both wheels are rolled out in opposite direction shown until they are 2660 cm apart. The two wheels need to make the same number of revolutions. How many revolutions does each wheel make assuming that each wheel must make a complete revolution? (Take π = 227)
Image in this question is not available.
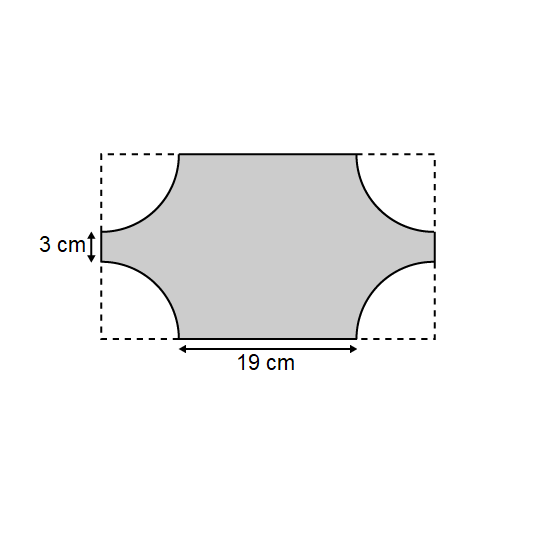
Level 3 The figure shows a rectangle with its corners cut out. Each of the 4 identical corners cut out is a quarter circle. The ratio of the length of the rectangle to its breadth is 13 : 5.
- What is the radius of each quarter circle?
- What is the perimeter of the shaded part. Take π = 3.14. Give your answer correct to 1 decimal place.
Level 3 The figure shows a rectangle with its corners cut out. Each of the 4 identical corners cut out is a quarter circle. The ratio of the length of the rectangle to its breadth is 13 : 5.
- What is the radius of each quarter circle?
- What is the perimeter of the shaded part. Take π = 3.14. Give your answer correct to 1 decimal place.
Image in this question is not available.
TRY FOR FREE
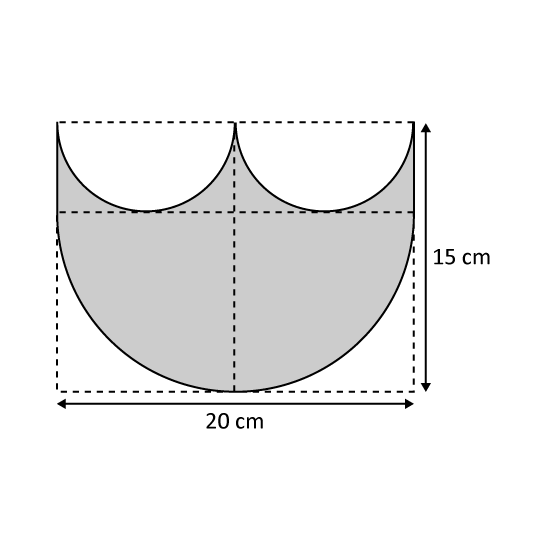
Level 2 PSLE A symmetric figure is drawn on a rectangular piece of paper 20 cm by 15 cm as shown. Its outline consists of a large semicircle, 2 smaller semicircles and 2 straight lines.
- What is the area of the figure?
- What is its perimeter? Take π = 3.14
Level 2 PSLE A symmetric figure is drawn on a rectangular piece of paper 20 cm by 15 cm as shown. Its outline consists of a large semicircle, 2 smaller semicircles and 2 straight lines.
- What is the area of the figure?
- What is its perimeter? Take π = 3.14
Image in this question is not available.
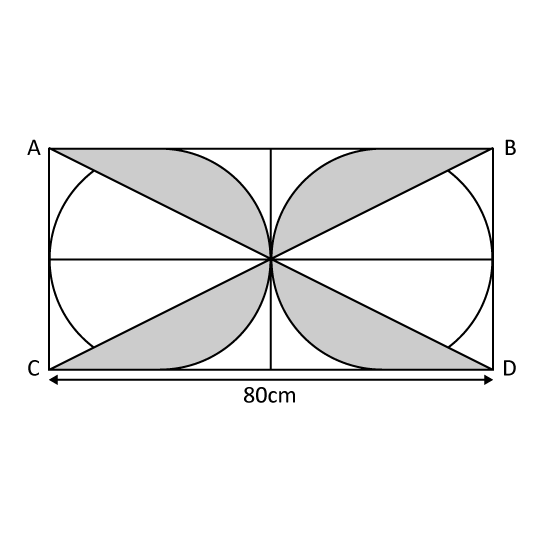
Level 3
The figure shows 2 identical circles enclosed in a rectangle ABCD. Find the area of the shaded parts. (Take π = 3.14)
Level 3
The figure shows 2 identical circles enclosed in a rectangle ABCD. Find the area of the shaded parts. (Take π = 3.14)
Image in this question is not available.
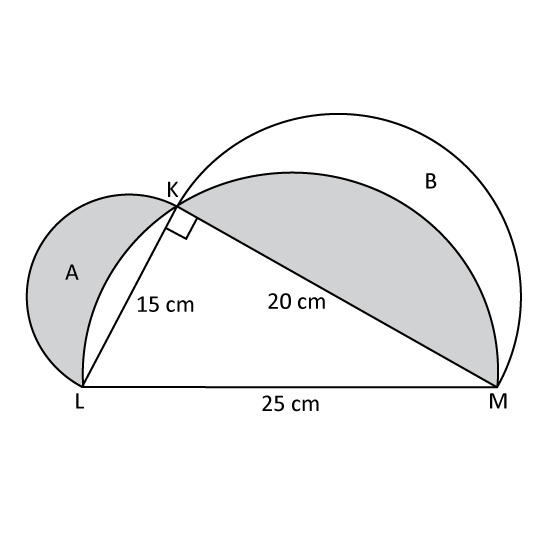
Level 3
The figure shows a triangle KLM and 3 semicircles. If the shaded area of the semicircle, labelled y, is 13 the unshaded area of the semicircle, labelled x, find the total shaded area. (Take π = 3.14)
Level 3
The figure shows a triangle KLM and 3 semicircles. If the shaded area of the semicircle, labelled y, is 13 the unshaded area of the semicircle, labelled x, find the total shaded area. (Take π = 3.14)
Image in this question is not available.
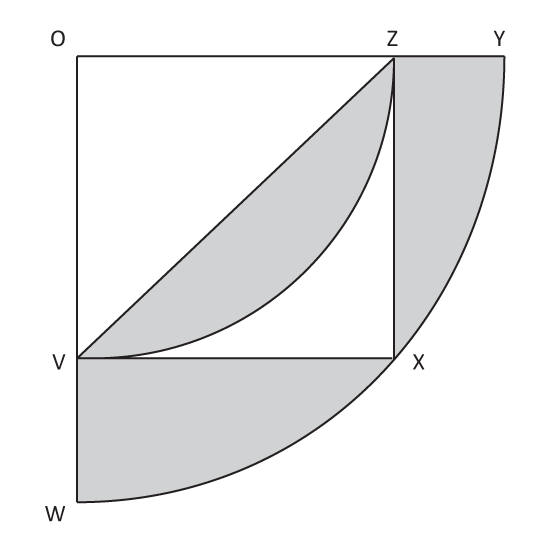
Level 3
The figure is made up of a big quadrant OWY a small quadrant OVZ and a square VXZO. The radius of the big quadrant OWY is 12cm. The area of the big quadrant is twice the area of the small quadrant OVZ. Using the calculator value of π, find the area of the shaded parts, correct to 2 decimal places.
Level 3
The figure is made up of a big quadrant OWY a small quadrant OVZ and a square VXZO. The radius of the big quadrant OWY is 12cm. The area of the big quadrant is twice the area of the small quadrant OVZ. Using the calculator value of π, find the area of the shaded parts, correct to 2 decimal places.
Image in this question is not available.
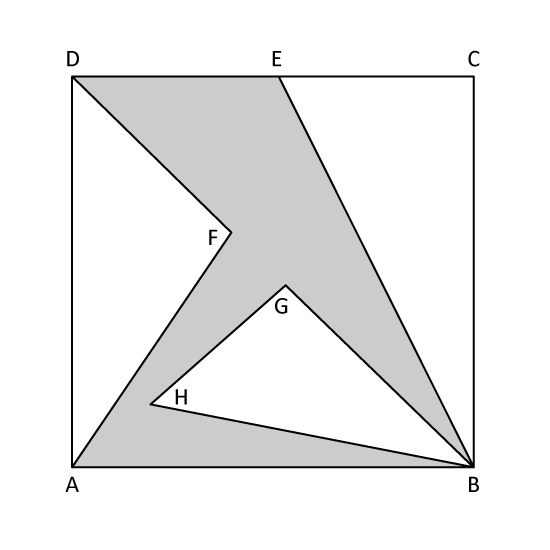
Level 3
In the figure, ABCD is a square of sides 24 cm. G is the midpoint of BD. DE = EC. DG is 4 times of FG. AH is 38 of AG. Find the total shaded area.
Level 3
In the figure, ABCD is a square of sides 24 cm. G is the midpoint of BD. DE = EC. DG is 4 times of FG. AH is 38 of AG. Find the total shaded area.
Image in this question is not available.
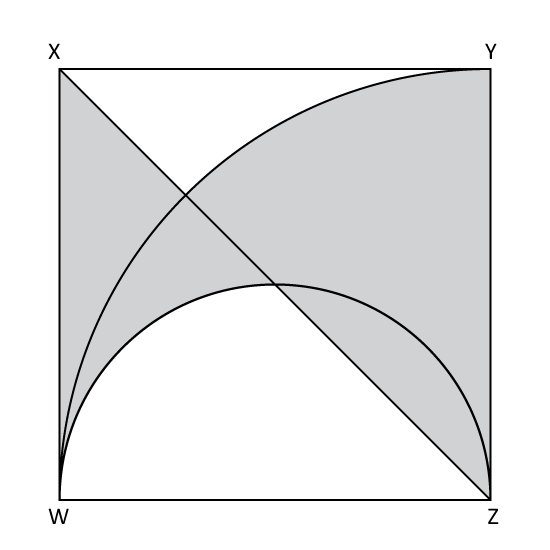
Level 3
The figure, not drawn to scale, is made up of a square, a quadrant and a semicircle. WXYZ is a square of side 28 cm. Find the area of the shaded part. (Take π = 227)
Level 3
The figure, not drawn to scale, is made up of a square, a quadrant and a semicircle. WXYZ is a square of side 28 cm. Find the area of the shaded part. (Take π = 227)
Image in this question is not available.
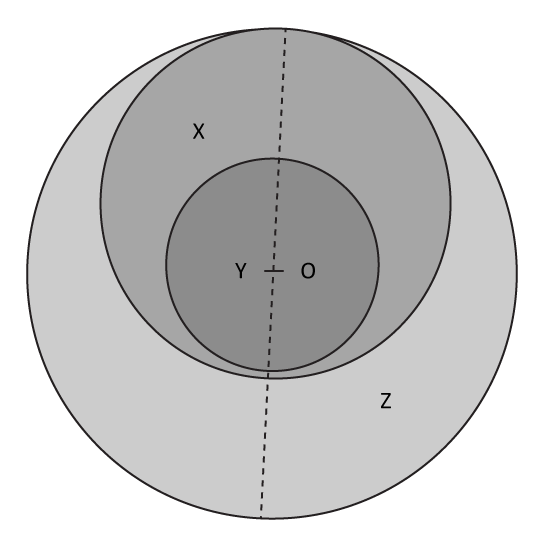
Level 3
The figure is make up of 3 circles. The small circle has centre O and a radius of 6 cm. The big circle, has centre O and a radius of 10 cm. The diameter of the big circle cuts through the centre of the medium-sized circle and the small circle. The three regions formed are indicated as X, Y and Z.
- Find the radius of the medium-sized circle.
- Find the area of region Z. Use a calculator to obtain the value of π.
(Round off to nearest 2 decimal places).
- Express the area of the region Y as a ratio to the area of region X.
Level 3
The figure is make up of 3 circles. The small circle has centre O and a radius of 6 cm. The big circle, has centre O and a radius of 10 cm. The diameter of the big circle cuts through the centre of the medium-sized circle and the small circle. The three regions formed are indicated as X, Y and Z.
- Find the radius of the medium-sized circle.
- Find the area of region Z. Use a calculator to obtain the value of π.
(Round off to nearest 2 decimal places).
- Express the area of the region Y as a ratio to the area of region X.
Image in this question is not available.
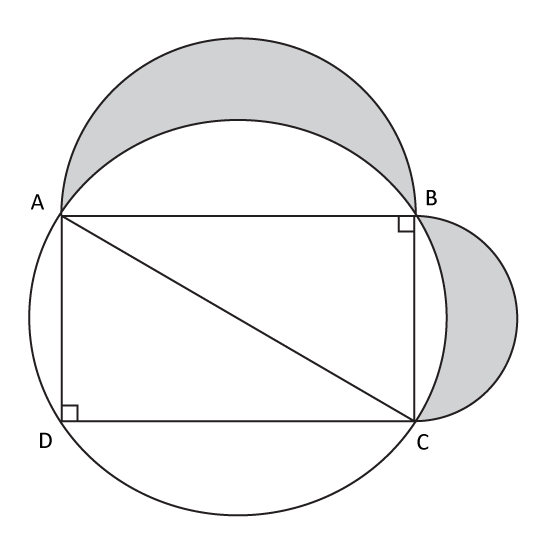
Level 3
The figure is made up of a circle, a rectangle and 2 semicircles. AC, the diameter of the circle, is 15 cm, AB is 12 cm and BC is 9 cm.
- What is the total area of the shaded parts?
- What is the total perimeter of the shaded parts?
(Take π = 3.14)
Level 3
The figure is made up of a circle, a rectangle and 2 semicircles. AC, the diameter of the circle, is 15 cm, AB is 12 cm and BC is 9 cm.
- What is the total area of the shaded parts?
- What is the total perimeter of the shaded parts?
(Take π = 3.14)
Image in this question is not available.
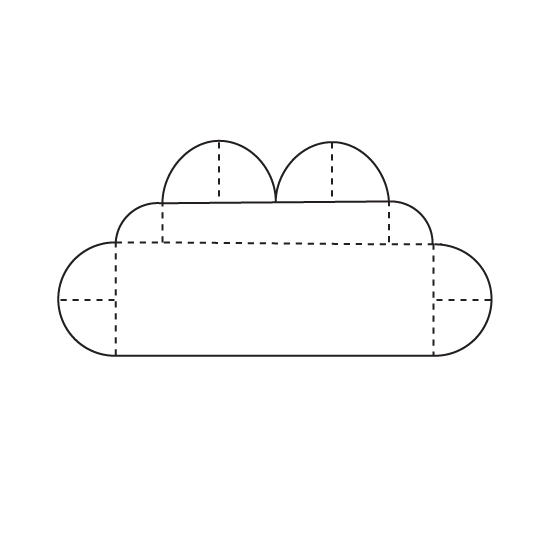
Level 3 PSLE The figure shows a table cloth. The outside edge of the mat is formed by 4 semicircles and 2 quarter circles, each of radius 14 cm.
- Find the perimeter of the mat.
- Find the area of the mat. Take π = 227.
Level 3 PSLE The figure shows a table cloth. The outside edge of the mat is formed by 4 semicircles and 2 quarter circles, each of radius 14 cm.
- Find the perimeter of the mat.
- Find the area of the mat. Take π = 227.
Image in this question is not available.
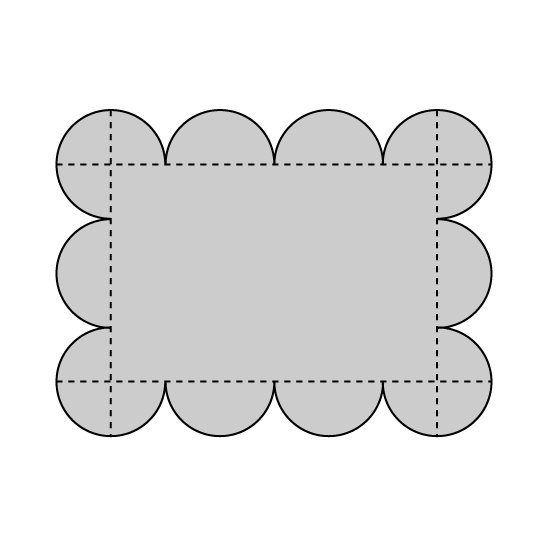
Level 3 PSLE The figure is made up of a rectangle, semicircles and quarter circles. The area of the rectangle is 216 cm
2.
- Find the perimeter of the rectangle.
- Find the area of the figure. Take π = 3.14
Level 3 PSLE The figure is made up of a rectangle, semicircles and quarter circles. The area of the rectangle is 216 cm
2.
- Find the perimeter of the rectangle.
- Find the area of the figure. Take π = 3.14
Image in this question is not available.
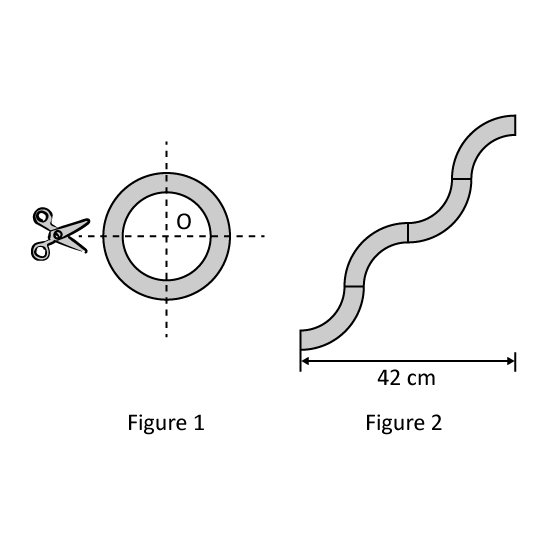
Level 3 PSLE
A small circle with centre O has been cut from a circular piece of cardboard with the same centre. The radius of the small circle is 8 cm.
The remaining cardboard is then cut into four equal parts along the dotted lines as shown in Figure 1. The four parts are rearranged to form a new shape in Figure 2.
- Find the area of the new shape.
- Find the perimeter of the new shape. (Take π = 3.14)
Level 3 PSLE
A small circle with centre O has been cut from a circular piece of cardboard with the same centre. The radius of the small circle is 8 cm.
The remaining cardboard is then cut into four equal parts along the dotted lines as shown in Figure 1. The four parts are rearranged to form a new shape in Figure 2.
- Find the area of the new shape.
- Find the perimeter of the new shape. (Take π = 3.14)
Image in this question is not available.
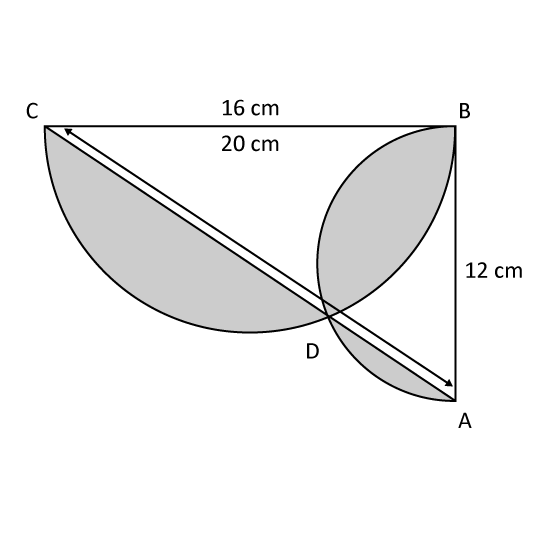
Level 3
The figure is made up of a right-angled triangle ABC and two semicircles with AB and BC as their diameters respectively. The two semicircles and the line AC meet at D as shown. AB = 12 cm. BC = 16 cm and AC = 20 cm. (Take π = 3.14)
- Find the perimeter of the shaded region. Correct the answer to 2 decimal places.
- Find the area of the shaded region.
Level 3
The figure is made up of a right-angled triangle ABC and two semicircles with AB and BC as their diameters respectively. The two semicircles and the line AC meet at D as shown. AB = 12 cm. BC = 16 cm and AC = 20 cm. (Take π = 3.14)
- Find the perimeter of the shaded region. Correct the answer to 2 decimal places.
- Find the area of the shaded region.
Image in this question is not available.
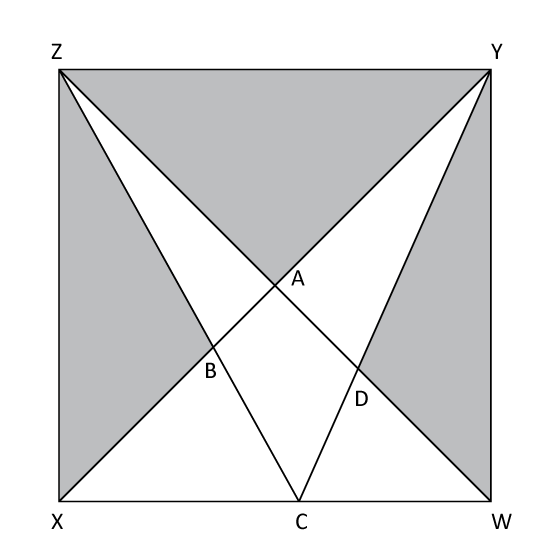
Level 3
In the figure, not drawn to scale, WXYZ is a rectangle with a length of 45 cm and a width of 22 cm. The area of the quadrilateral ABCD is 75 cm2.
Find the ratio of the shaded area to the unshaded area.
Level 3
In the figure, not drawn to scale, WXYZ is a rectangle with a length of 45 cm and a width of 22 cm. The area of the quadrilateral ABCD is 75 cm2.
Find the ratio of the shaded area to the unshaded area.
Image in this question is not available.
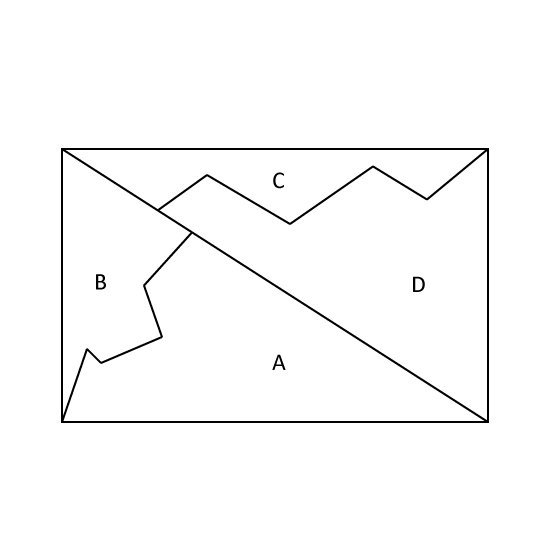
Level 3
The rectangle is divided into four parts A, B, C and D.
The ratio of Part A to Part B is 5 : 3 and the ratio of Part B to Part C is 2 : 1.
- Find the ratio of Part A to Part B to Part C.
- Given that Part D is 26 cm2 , find the area of the rectangle.
Level 3
The rectangle is divided into four parts A, B, C and D.
The ratio of Part A to Part B is 5 : 3 and the ratio of Part B to Part C is 2 : 1.
- Find the ratio of Part A to Part B to Part C.
- Given that Part D is 26 cm2 , find the area of the rectangle.
Image in this question is not available.