Level 3
The figure, not drawn to scale, is made up of two identical right-angled triangles, a small square and a big square. The lengths of the 2 squares are whole numbers. The perimeter of the shaded region is 32 cm, and the total area of the two unshaded squares is 89 cm2. Find the total area of the two shaded right-angled triangles.
Level 3
The figure, not drawn to scale, is made up of two identical right-angled triangles, a small square and a big square. The lengths of the 2 squares are whole numbers. The perimeter of the shaded region is 32 cm, and the total area of the two unshaded squares is 89 cm2. Find the total area of the two shaded right-angled triangles.
Image in this question is not available.
Level 3
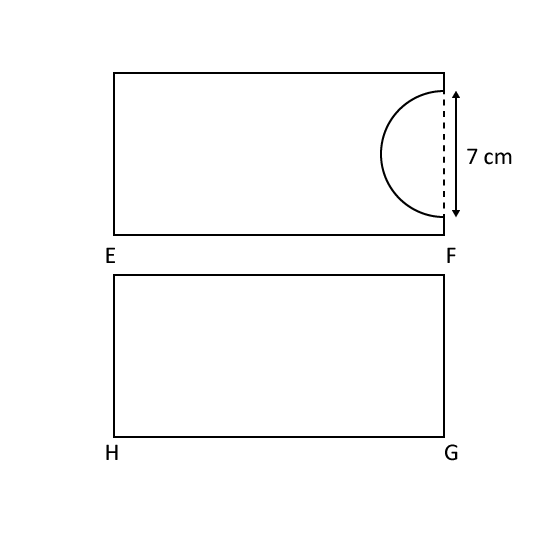
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Level 3
- The figure shows a rectangular field EFGH. Mike walked from E to F to G to H and he covered a distance of 57m. Sandy walked from F to G to H to E and she covered a distance of 48m. What is the perimeter of the field?
- Some construction work was undertaken to the same field and a semi-circular part was removed from it. What is the perimeter of the field after the construction? (Take π = 227)
Image in this question is not available.
Level 3
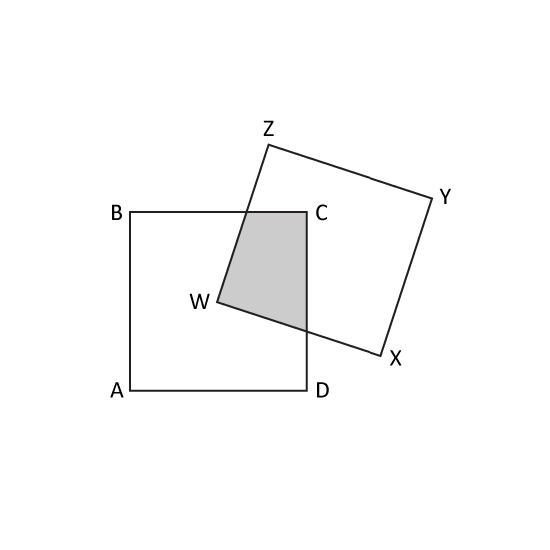
The figure, not drawn to scale, is made up of 2 identical squares, ABCD and WXYZ. The length of each square is 10 cm. Point W is the centre of square ABCD.
- What fraction of the figure is shaded?
- What is the area of the unshaded parts?
Level 3
The figure, not drawn to scale, is made up of 2 identical squares, ABCD and WXYZ. The length of each square is 10 cm. Point W is the centre of square ABCD.
- What fraction of the figure is shaded?
- What is the area of the unshaded parts?
Image in this question is not available.
Level 3 PSLE
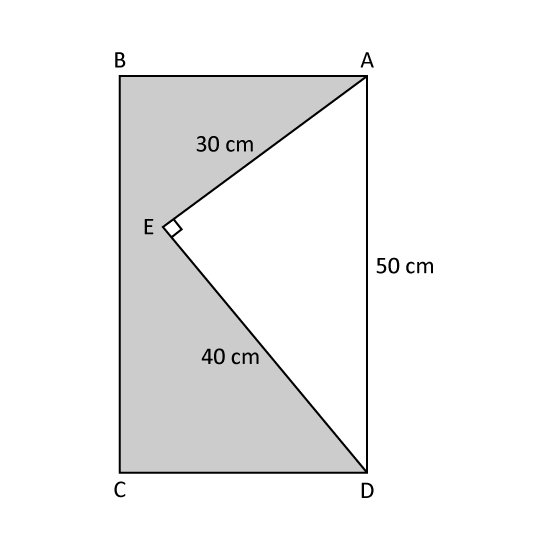
In the figure, ABCD is a rectangle and AED is a right-angled triangle with sides measuring 30 cm, 40 cm and 50 cm. The perimeter of the shaded part is 176 cm. What is the ratio of the area of the triangle to the area of the shaded part? Give your answer in the simplest form.
Level 3 PSLE
In the figure, ABCD is a rectangle and AED is a right-angled triangle with sides measuring 30 cm, 40 cm and 50 cm. The perimeter of the shaded part is 176 cm. What is the ratio of the area of the triangle to the area of the shaded part? Give your answer in the simplest form.
Image in this question is not available.
Level 3
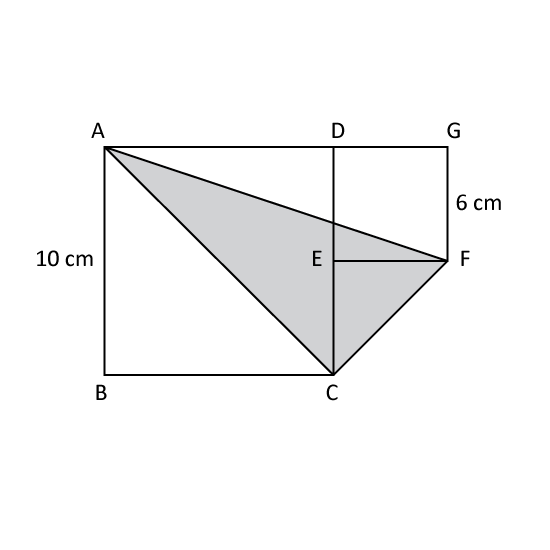
In the figure, ABCD and DEFG are squares. Find the area of the shaded triangle ACF.
Level 3
In the figure, ABCD and DEFG are squares. Find the area of the shaded triangle ACF.
Image in this question is not available.
Level 3 PSLE
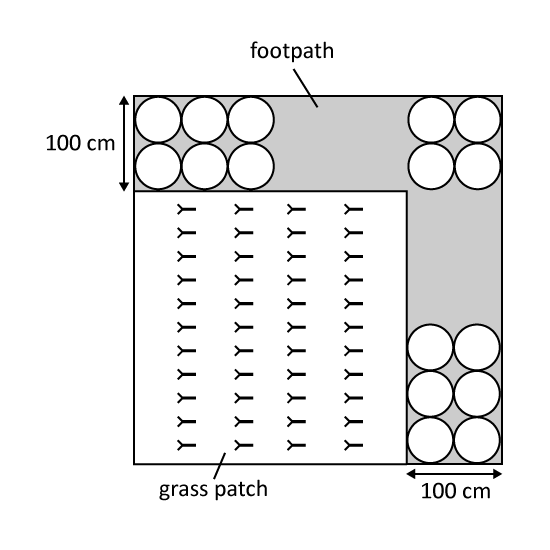
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Level 3 PSLE
The figure shows a rectangular grass patch and an L-shaped footpath. The width of the footpath is 100 cm. The footpath is tiled using 38 circular tiles of diameter 50 cm, following the pattern shown. Each tile is in contact with those next to it.
- What is the area of the footpath not covered by the tiles? Take π = 3.14.
- What is the perimeter of the grass patch?
Image in this question is not available.
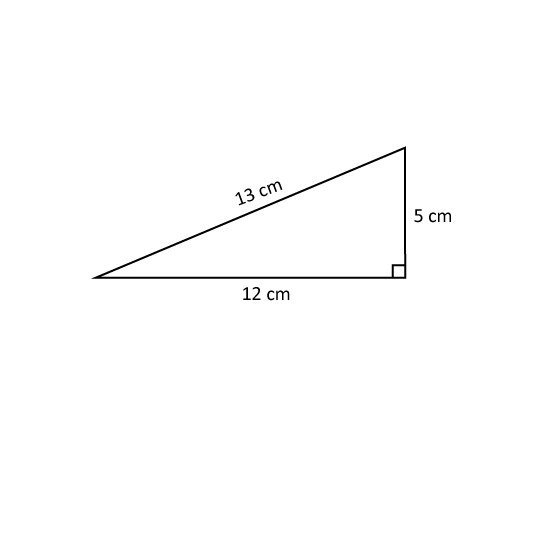
Level 3 PSLE The figure shows a right-angled triangle.
- Find the area of the triangle.
- Bruce wants to cut such triangles from a rectangular piece of cardboard 50 cm by 80 cm. At most, how many of such triangles can he cut?
Level 3 PSLE The figure shows a right-angled triangle.
- Find the area of the triangle.
- Bruce wants to cut such triangles from a rectangular piece of cardboard 50 cm by 80 cm. At most, how many of such triangles can he cut?
Image in this question is not available.
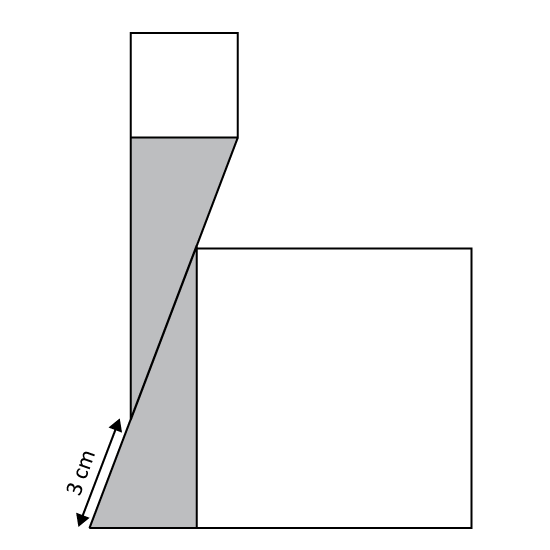
Level 3
Find the area of the figure.
Level 3
Find the area of the figure.
Image in this question is not available.
Level 3
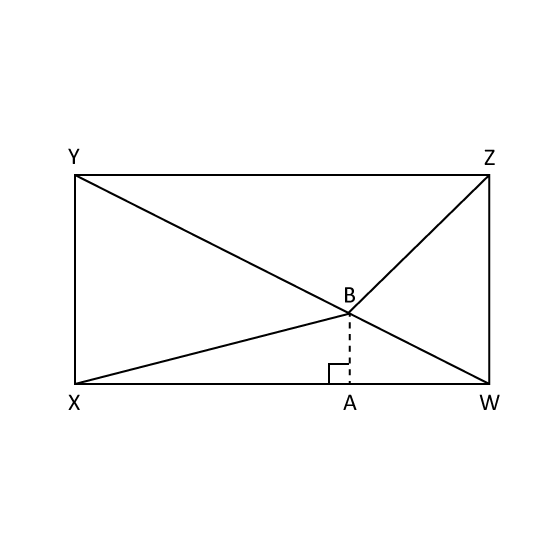
The figure shows a rectangle WXYZ. The lines are extended from point W, X, Y and Z and they meet at point B. The length of YZ is 30 cm. Given that the area of triangle WBZ is 65 cm2 and the area of triangle XBY is 105 cm2, find the breadth of the rectangle in mixed number.
Level 3
The figure shows a rectangle WXYZ. The lines are extended from point W, X, Y and Z and they meet at point B. The length of YZ is 30 cm. Given that the area of triangle WBZ is 65 cm2 and the area of triangle XBY is 105 cm2, find the breadth of the rectangle in mixed number.
Image in this question is not available.
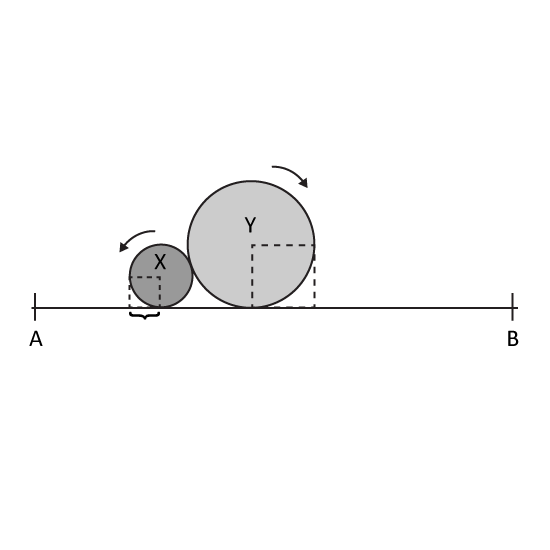
Level 3
The figure is not drawn to scale. Two balls, X and Y, turn and move along the line AB in opposite directions. The radius of X is 10 cm. The ratio of the diameter of Ball X to that of Ball Y is 5 : 2. If Ball X turns 10 rounds and Ball Y turns 2 rounds, how far apart are the centres of the balls?
(Take π = 3.14)
Level 3
The figure is not drawn to scale. Two balls, X and Y, turn and move along the line AB in opposite directions. The radius of X is 10 cm. The ratio of the diameter of Ball X to that of Ball Y is 5 : 2. If Ball X turns 10 rounds and Ball Y turns 2 rounds, how far apart are the centres of the balls?
(Take π = 3.14)
Image in this question is not available.
Level 3
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Level 3
The figure shows 4 similar right-angled triangles arranged to form a big square which encloses a circle. The midpoints of the 4 sides of the big square touch the circumference of the circle. The two sides which form the right angle of each triangle are 16 cm and 12 cm respectively. Find the area of the shaded part. (Take π = 3.14)
Image in this question is not available.
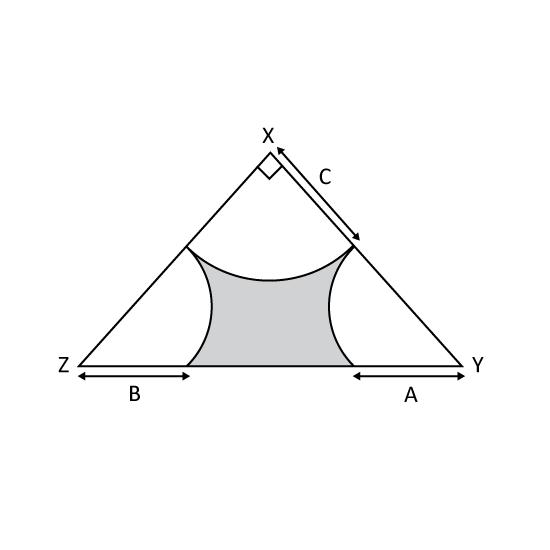
Level 3
The figure is not drawn to scale. A, B and C are radii of 21 cm long. Find the area of the shaded part. (Take π = 227)
Level 3
The figure is not drawn to scale. A, B and C are radii of 21 cm long. Find the area of the shaded part. (Take π = 227)
Image in this question is not available.
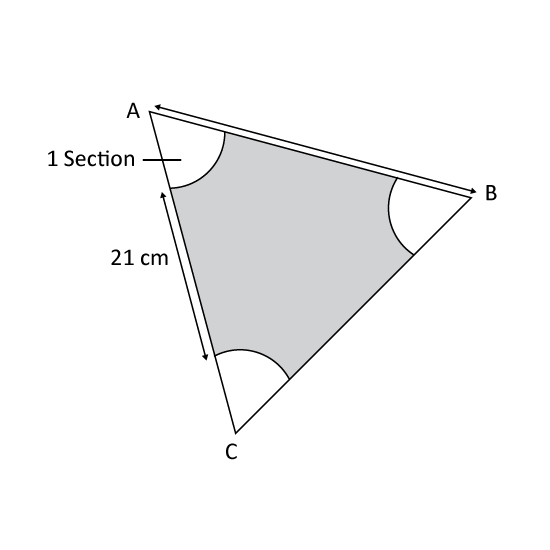
Level 3
Three similar sections are cut away from an equilateral cardboard triangle ABC. Each side of the equilateral triangle is 56 cm. Find the perimeter of the remaining cardboard. (Take π = 3.14)
Level 3
Three similar sections are cut away from an equilateral cardboard triangle ABC. Each side of the equilateral triangle is 56 cm. Find the perimeter of the remaining cardboard. (Take π = 3.14)
Image in this question is not available.
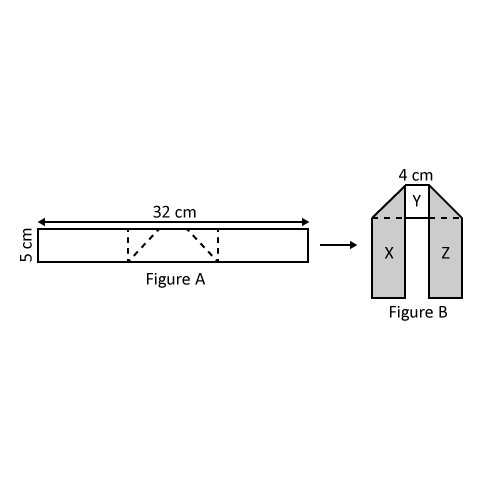
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Level 3
The figure shows a rectangular piece of paper 32 cm by 5 cm which is coloured on one side. It is folded along the dotted line to form Figure B.
- Find the area of the rectangular piece of paper.
- Find the total area of X, Y and Z in Figure B.
Image in this question is not available.
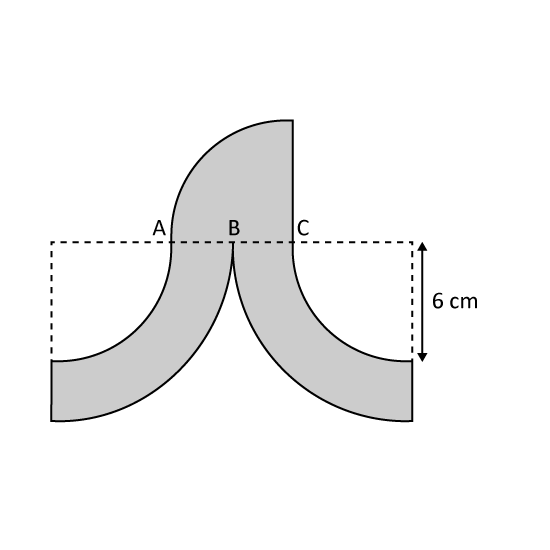
Level 2 PSLE The outline of the shaded figure is formed by 3 identical small quarter circles, 2 identical large quarter circles and 3 straight lines. Take π = 3.14
- What is the radius of the large quarter circle?
- Find the perimeter of the shaded figure.
Level 2 PSLE The outline of the shaded figure is formed by 3 identical small quarter circles, 2 identical large quarter circles and 3 straight lines. Take π = 3.14
- What is the radius of the large quarter circle?
- Find the perimeter of the shaded figure.
Image in this question is not available.
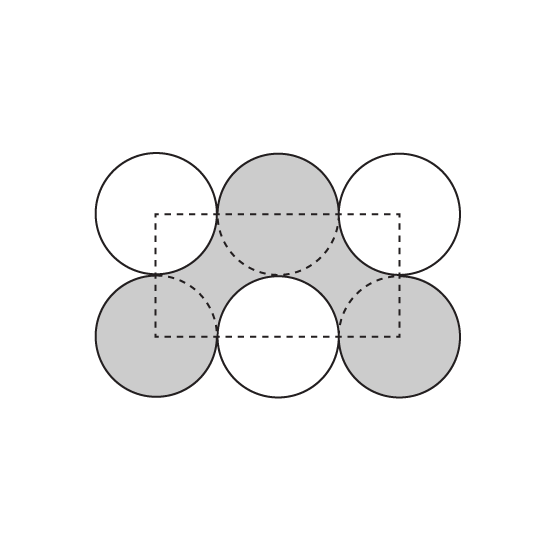
Level 3 PSLE The figure shows 6 circles, each of radius 7 cm. Each circle touches the circles next to it.
(Take π =
227)
- Find the perimeter of the shaded part.
- Find the area of the shaded part.
Level 3 PSLE The figure shows 6 circles, each of radius 7 cm. Each circle touches the circles next to it.
(Take π =
227)
- Find the perimeter of the shaded part.
- Find the area of the shaded part.
Image in this question is not available.
TRY FOR FREE
Level 3 PSLE
A plot of land which had an area of 876 m
2 was divided into three portions of equal width. These portions were fenced using 177 m of fence as shown.
- Find the length of AB.
- Find the perimeter of the plot of land.
Level 3 PSLE
A plot of land which had an area of 876 m
2 was divided into three portions of equal width. These portions were fenced using 177 m of fence as shown.
- Find the length of AB.
- Find the perimeter of the plot of land.
Image in this question is not available.
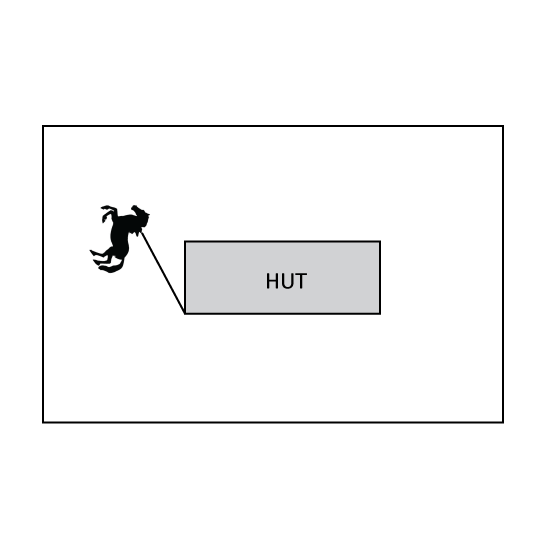
Level 3
On a rectangular plot, a horse is tied to a pole at a corner of the hut which measures 18 m by 6 m. The hut is at the centre of the rectangular grass patch and there is a 14 m wide border of grass patch around it. Given that the rope is 12 m long,
- what is the maximum grass patch area that the horse can feed on?
- find the total area of the grass patch that the horse cannot feed on.
(Take π = 3.14)
Level 3
On a rectangular plot, a horse is tied to a pole at a corner of the hut which measures 18 m by 6 m. The hut is at the centre of the rectangular grass patch and there is a 14 m wide border of grass patch around it. Given that the rope is 12 m long,
- what is the maximum grass patch area that the horse can feed on?
- find the total area of the grass patch that the horse cannot feed on.
(Take π = 3.14)
Image in this question is not available.
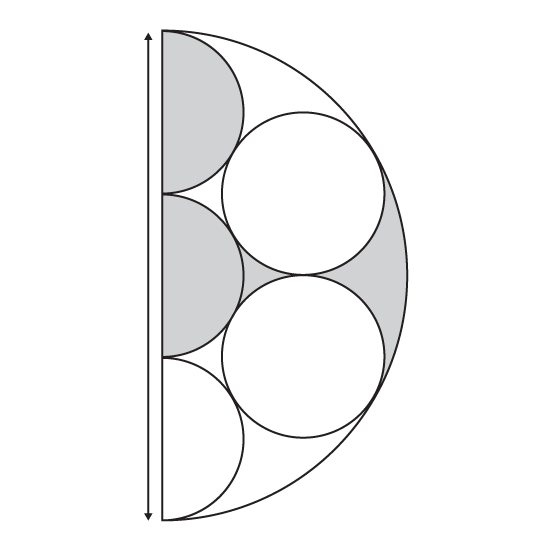
Level 3
A piece of rope is used to make the figure shown. Inside the big semicircle are 2 small circles and 3 small semi-circles, all of which have the same radius. The diameter of the big semicircle is 30 cm. Find the area of the shaded region. (Leave the answer in terms of π)
Level 3
A piece of rope is used to make the figure shown. Inside the big semicircle are 2 small circles and 3 small semi-circles, all of which have the same radius. The diameter of the big semicircle is 30 cm. Find the area of the shaded region. (Leave the answer in terms of π)
Image in this question is not available.
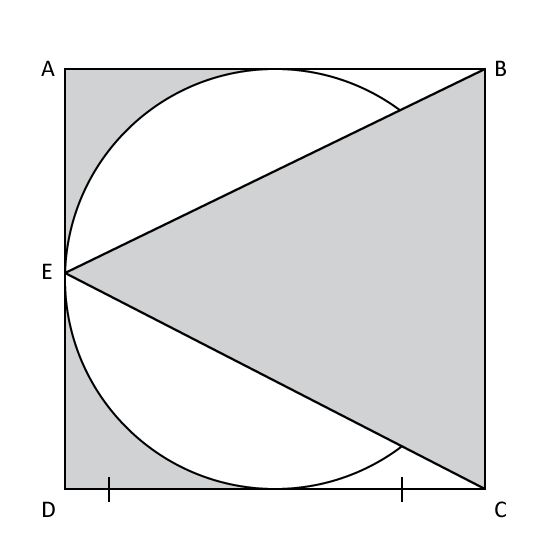
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Level 3
The figure is made up of a circle, a triangle and a square of sides 28 cm. E is the mid-point of AD. Find the area of the shaded region. (Take π = 227)
Image in this question is not available.