Level 2 PSLE
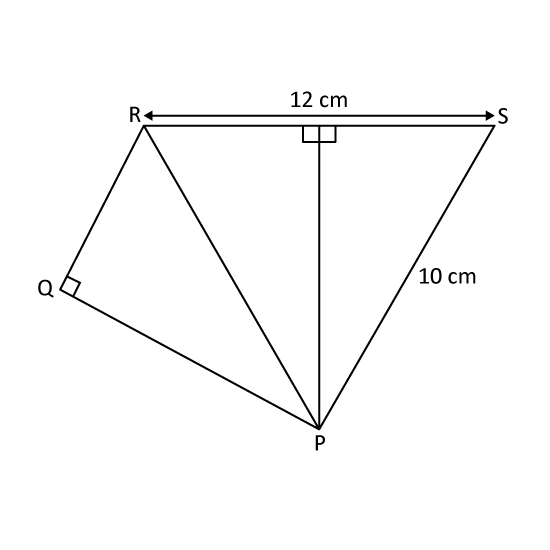
Robert cut out three identical right-angled triangles. He joined them to form the figure PQRS shown. RS = 12 cm and SP = 10 cm. The perimeter of the figure is 36 cm. Find the area of the figure PQRS.
Level 2 PSLE
Robert cut out three identical right-angled triangles. He joined them to form the figure PQRS shown. RS = 12 cm and SP = 10 cm. The perimeter of the figure is 36 cm. Find the area of the figure PQRS.
Image in this question is not available.
Level 2
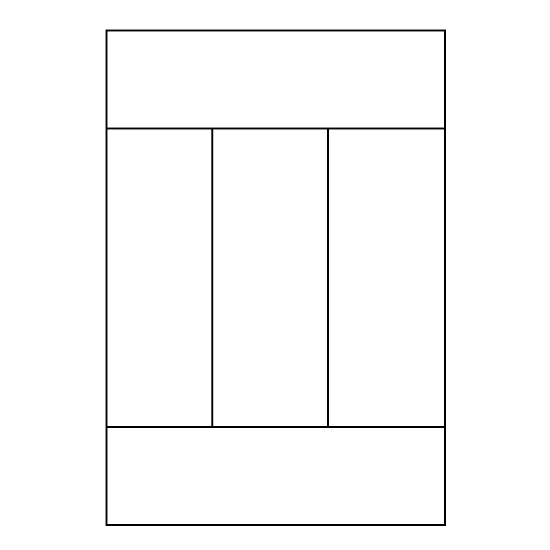
The figure is made up of 5 identical rectangles with a perimeter of 336 cm. Find the area of each rectangle.
Level 2
The figure is made up of 5 identical rectangles with a perimeter of 336 cm. Find the area of each rectangle.
Image in this question is not available.
Level 2
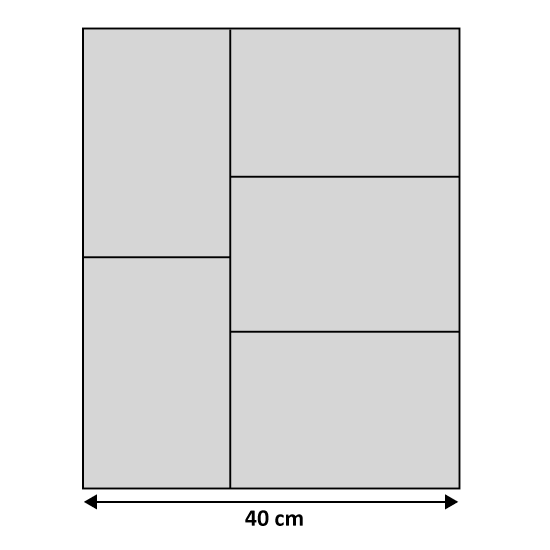
A rectangular paper can be divided into 5 identical small rectangles as shown. Given that the breadth of the paper is 40cm, find the area.
Level 2
A rectangular paper can be divided into 5 identical small rectangles as shown. Given that the breadth of the paper is 40cm, find the area.
Image in this question is not available.
Level 2
W, X, Y and Z are mid-points of the sides of the square. If the area of the square is 100 cm2, what is the area of the unshaded triangles? Leave your answer in mixed number.
Level 2
W, X, Y and Z are mid-points of the sides of the square. If the area of the square is 100 cm2, what is the area of the unshaded triangles? Leave your answer in mixed number.
Image in this question is not available.
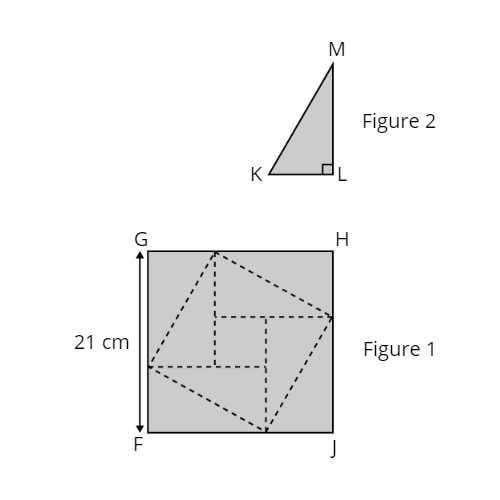
Level 2 PSLE
Anna has a square piece of paper FGHJ of side 21 cm. She cut along the dotted lines shown in Figure 1 to get one small square of area 9 cm2 and 8 identical right-angled triangles. Triangle KLM in Figure 2 is one such triangle. Find the length of KM.
Level 2 PSLE
Anna has a square piece of paper FGHJ of side 21 cm. She cut along the dotted lines shown in Figure 1 to get one small square of area 9 cm2 and 8 identical right-angled triangles. Triangle KLM in Figure 2 is one such triangle. Find the length of KM.
Image in this question is not available.
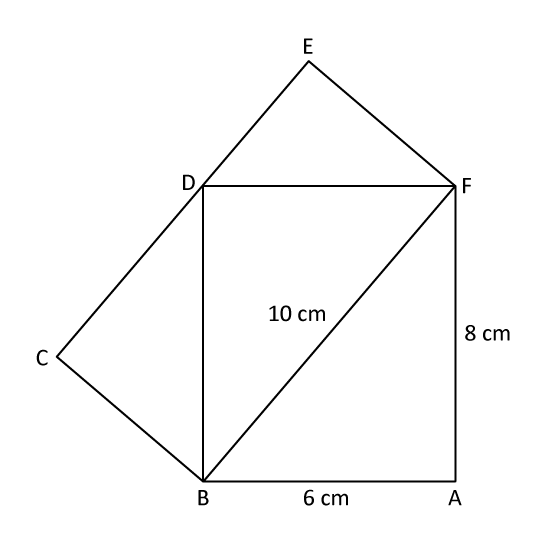
Level 2 PSLE
In the figure, ABDF and BCEF are rectangles and CDE is a straight line. AB = 6 cm, AF = 8 cm and BF = 10 cm. Find the length of BC.
Level 2 PSLE
In the figure, ABDF and BCEF are rectangles and CDE is a straight line. AB = 6 cm, AF = 8 cm and BF = 10 cm. Find the length of BC.
Image in this question is not available.
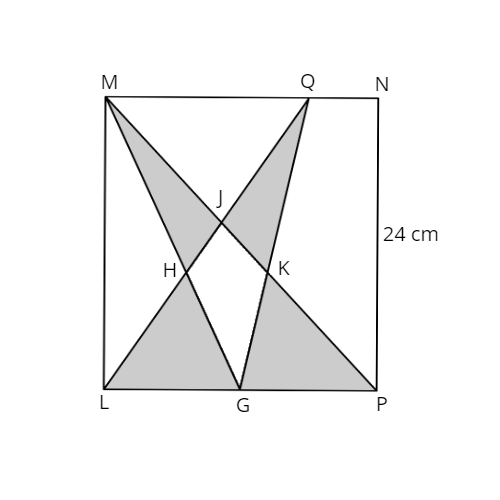
Level 2
The figure is not drawn to scale. Given that GL = GP, NM = 18 cm and the area of GHJK is 45 cm2, find the area of the shaded parts.
Level 2
The figure is not drawn to scale. Given that GL = GP, NM = 18 cm and the area of GHJK is 45 cm2, find the area of the shaded parts.
Image in this question is not available.
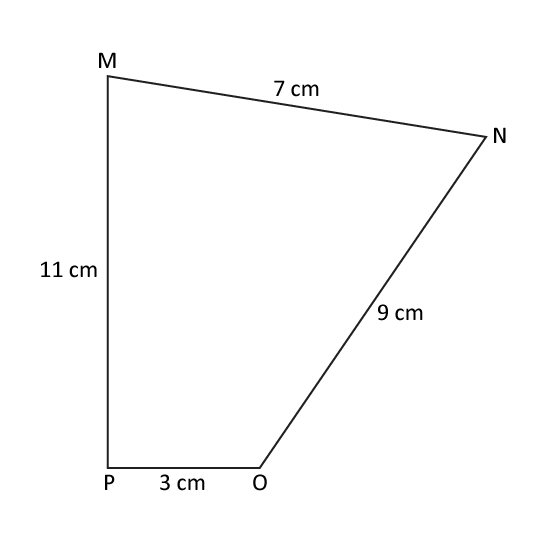
Level 2 PSLE
In the figure, MN = 7 cm, NO = 9 cm, OP = 3 cm and PM = 11 cm. ∠MNO and ∠OPM are right angles. Find the area of the figure MNOP.
Level 2 PSLE
In the figure, MN = 7 cm, NO = 9 cm, OP = 3 cm and PM = 11 cm. ∠MNO and ∠OPM are right angles. Find the area of the figure MNOP.
Image in this question is not available.
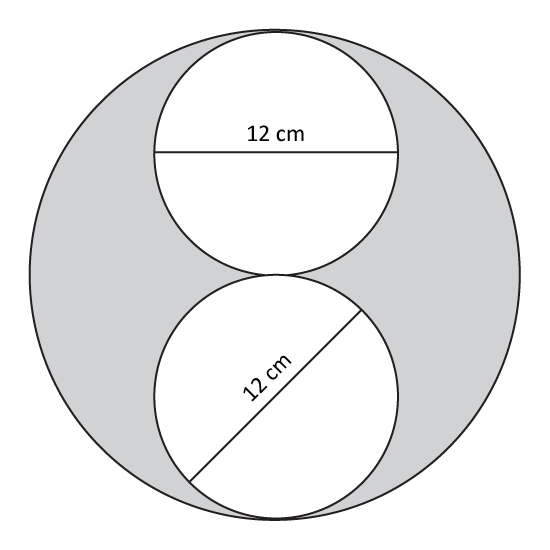
Level 2
The figure shows 2 identical small circles of diameter 12 cm inside a big circle of radius 12 cm. Find the area of the unshaded part of the big circle. Express the answer in terms of π.
Level 2
The figure shows 2 identical small circles of diameter 12 cm inside a big circle of radius 12 cm. Find the area of the unshaded part of the big circle. Express the answer in terms of π.
Image in this question is not available.
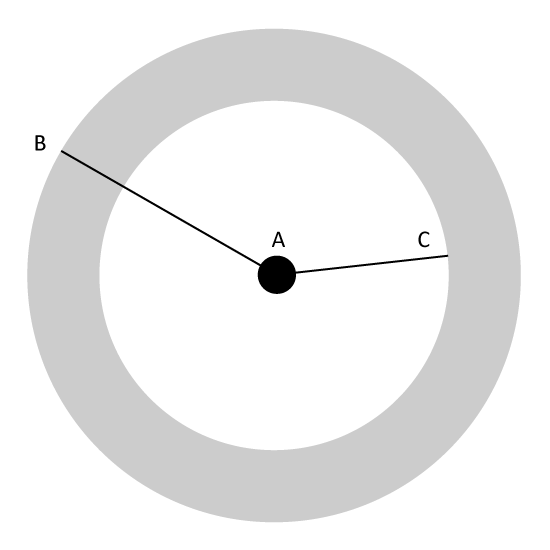
Level 2
The figure (not drawn to scale) is made of two concentric circles. AB is the radius of the bigger circle. AC is the radius of the smaller circle. AB is 35 cm while AC is 14 cm. Find the area of the shaded region. (Take π = 227)
Level 2
The figure (not drawn to scale) is made of two concentric circles. AB is the radius of the bigger circle. AC is the radius of the smaller circle. AB is 35 cm while AC is 14 cm. Find the area of the shaded region. (Take π = 227)
Image in this question is not available.